
分析 设M(x0,y0),B1(0,-2),B2(0,2),求出直线MB1,MB2,从而求出P,Q两点坐标,由此能求出|OP|•|OQ|的值.
解答 解:设M(x0,y0),B1(0,-2),B2(0,2),
∴${k_{M{B_1}}}=\frac{{{y_0}+2}}{x_0}$,
∴${l_{M{B_1}}}:y+2=\frac{{{y_0}+2}}{x_0}•x$,
∵y=0,
∴${x_P}=\frac{{2{x_0}}}{{{y_0}+2}}$,
同理,${l_{M{B_2}}}:y+2=\frac{{{y_0}-2}}{x_0}•x⇒{x_Q}=\frac{{2{x_0}}}{{{y_0}-2}}$,
∴$|OP|•|OQ|=|{x_P}|•|{x_Q}|=\frac{4x_0^2}{|y_0^2-4|}$,
∵$\frac{x_0^2}{9}+\frac{y_0^2}{4}=1⇒4-y_0^2=\frac{4}{9}x_0^2$,
∴|OP|•|OQ|=9.
点评 本题考查两线段长的求法,是中档题,解题时要认真审题,注意直线方程、椭圆性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x≥1或 x≤-1,则 x2≥1 | B. | 若-1<x<1,则 x2<1 | ||
| C. | 若x>1或x<-1,则 x2>1 | D. | 若 x2≥1,则 x≥1或 x≤-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
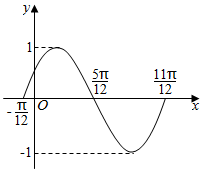
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com