Question

【题目】如图，几何体是圆柱的一部分，它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的，G是的中点.

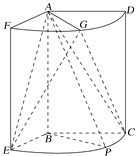
(1)设P是上的一点，且AP⊥BE，求∠CBP的大小；

(2)当AB＝3，AD＝2时，求二面角E－AG－C的大小.

Answer 1

【答案】（1）；（2）

【解析】试题分析: (1)第(1)问,直接证明BE⊥平面ABP得到BE⊥BP,从而求出∠CBP的大小. (2)第（2）问，可以利用几何法求，也可以利用向量法求解.

试题解析：

(1)

因为AP⊥BE，AB⊥BE，AB，AP平面ABP，AB∩AP＝A，所以BE⊥平面ABP.

又BP平面ABP，所以BE⊥BP.又∠EBC＝120°，所以∠CBP＝30°.

(2)方法一：如图，取的中点H，连接EH，GH，CH.

因为∠EBC＝120°，所以四边形BEHC为菱形，

所以AE＝GE＝AC＝GC＝.

取AG的中点M，连接EM，CM，EC，

则EM⊥AG，CM⊥AG，

所以∠EMC为所求二面角的平面角．

又AM＝1，所以EM＝CM＝.

在△BEC中，由于∠EBC＝120°，

由余弦定理得EC2＝22＋22－2×2×2×cos 120°＝12，

所以EC＝2，所以△EMC为等边三角形，

故所求的角为60°.

方法二：

以B为坐标原点，分别以BE，BP，BA所在的直线为x，y，z轴，建立如图所示的空间直角坐标系B－xyz.

由题意得A(0,0,3)，E(2,0,0)，G(1， ，3)，C(－1， ，0)，

故＝(2,0，－3)， ＝(1， ，0)， ＝(2,0,3)．

设＝(x1，y1，z1)是平面AEG的一个法向量，

由可得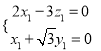

取z1＝2，可得平面AEG的一个法向量＝(3，－ ，2)．

设＝(x2，y2，z2)是平面ACG的一个法向量．

由可得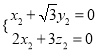

取z2＝－2，得平面ACG的一个法向量n＝(3，－ ，－2)．

所以cos〈〉＝＝.

故所求的角为60°.