黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案科目：高中数学 来源： 题型：解答题
若f(x)的定义域为[a,b]，值域为[a,b]（a<b），则称函数f(x)是[a,b]上的“四维光军”函数.
①设g(x)＝
x2－x+
是[1，b]上的“四维光军”函数，求常数b的值;
②问是否存在常数a，b（a>－2），使函数h(x)=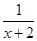
是区间[a,b]上的“四维光军”函数？若存在，求出a,b的值，否则，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知某公司生产某品牌服装的年固定成本为10万元，每生产千件需另投入2.7万元，设该公司年内共生产该品牌服装千件并全部销售完，每千件的销售收入为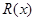
万元，且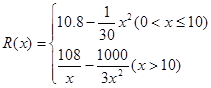
．
(1）写出年利润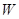
（万元）关于年产品（千件）的函数解析式；
(2）年产量为多少千件时，该公司在这一品牌服装的生产中所获年利润最大？
(注：年利润=年销售收入－年总成本）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某纺纱厂生产甲、乙两种棉纱，已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨；生产乙种棉纱1吨需耗一级籽棉1吨，二级籽棉2吨.每1吨甲种棉纱的利润为900元，每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中，要求消耗一级籽棉不超过250吨，二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨，能使利润总额最大？并求出利润总额的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（II）
，其中常数a > 0．
上是减函数；
是定义在
上的偶函数，且
时，
． 
，
；
，求
的取值范围．
.
，
．
，求证：函数
是
上的奇函数；
上没有零点，求实数
的取值范围．
，
，求
的范围； （2）不等式
对任意
恒成立，求实数
的取值范围。