
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
科目:高中数学 来源: 题型:解答题
已知函数f(x)=|x+1|,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x)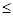 g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,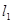 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系;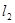 表示摩托车厂一天的销售成本与销售量的关系.
表示摩托车厂一天的销售成本与销售量的关系.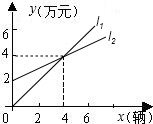
(1)写出销售收入与销售量之间的函数关系式;
(2)写出销售成本与销售量之间的函数关系式;
(3)当一天的销售量为多少辆时,销售收入等于销售成本;
(4)当一天的销售超过多少辆时,工厂才能获利?(利润=收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数 和
和 的图像如图所示,设两函数的图像交于点
的图像如图所示,设两函数的图像交于点 .
.
(1)请指出示意图中曲线 分别对应哪一个函数?
分别对应哪一个函数?
(2) ,且
,且 ,指出
,指出 的值,并说明理由;
的值,并说明理由;
(3)结合函数图像示意图,请把
四个数按从小到大的顺序排列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com