练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．方程组$\left\{\begin{array}{l}x+y=3\\ x-y=1\end{array}\right.$的解集为（　　）
    A．{x=2，y=1}B．$\left\{{\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.}\right\}$C．{2，1}D．{（2，1）}

    分析 利用“消元法”即可得出．

    解答 解：$\left\{\begin{array}{l}{x+y=3}&{①}\\{x-y=1}&{②}\end{array}\right.$，
    ①+②可得：2x=4，解得x=2，把x=2代入①可得2+y=3，解得y=1．
    ∴方程组$\left\{\begin{array}{l}x+y=3\\ x-y=1\end{array}\right.$的解集为{（2，1）}，
    故选：D．

    点评 本题考查了方程组的解法、“消元法”，考查了计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

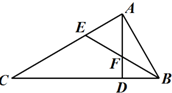    17．如图所示，在△ABC中，∠CAB=90°，AD⊥BC于D，BE是∠ABC的平分线，交AD于F，已知DF=$\sqrt{2}$，AF=$\sqrt{5}$，EC=2$\sqrt{5}$，则AE=2$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=|x-2|-|x+1|．
    （1）解不等式：f（x）≥2；
    （2）若?x0∈R，使得f（x0）≥m，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．一个半径为1的扇形OAB，其弦AB的长为d，面积为t，则函数d=f （t ） 的图象大致是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在棱长为1的正方体ABCD-A1B1C1D1中，O是正方体中心，N是棱A1B1上一点，P为正方体的表面动点，若满足OP⊥BN的P点轨迹为曲线E，则当N在棱A1B1上运动时，曲线E周长的取值范围是$[{4，2+2\sqrt{2}}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．函数y=$\sqrt{{x}^{2}+9}$的值域为（　　）
    A．RB．[3，+∞）C．[0，+∞）D．[9，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．如图，矩形ABEF所在的平面与等边△ABC所在的平面垂直，AB=2，AF=1，O为AB的中点．
    （1）求证：OE⊥FC；
    （2）求二面角F-CE-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．圆心在抛物线y2=2x（y≥0）上，经过点（2，0）且面积最小的圆为⊙C，直线y=kx+2与⊙C相交于A，B两点，当弦长|AB|取得最小值时k=$\frac{2+\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机抽调了50人，他们年龄的频数分布及支持“生育二胎”人数如下表：
    年龄[5，15）[15，25）[25，35）[35，45）[45，55）[55，65）
    频数510151055
    支持“生育二胎”4512821
    （Ⅰ）由以上统计数据填下面2×2列联表；
    年龄不低于45岁的人年龄低于45岁的人合计
    支持“生育二胎”a=3c=2932
    不支持“生育二胎”b=7d=1118
    合计1040n=50
    （Ⅱ）判断是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异．
    P（K2≥k）0.0500.0100.001
    k3.8416.63510.828
    附表：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    同步练习册答案