
分析 (1)利用绝对值的几何意义,分类讨论,即可解不等式:f(x)≥2;
(2)若?x0∈R,使得f(x0)≥m,等价于f(x)max≥m,即可求实数m的取值范围.
解答 解:(1)由题意,|x-2|-|x+1|≥2.
x<-1,不等式可化为2-x+x+1≥2,成立,∴x<-1;
-1≤x≤2,不等式可化为2-x-x-1≥2,解得x≤-$\frac{1}{2}$,∴-1≤x≤-$\frac{1}{2}$;
x>2,不等式可化为x-2-x-1≥2,无解;
综上所述,不等式的解集为(-∞,-$\frac{1}{2}$];
(2)?x0∈R,使得f(x0)≥m,等价于f(x)max≥m,
∵f(x)=|x-2|-|x+1|≤|x-2-x-1|=3,
∴m≤3.
点评 本题考查绝对值不等式,考查绝对值三角不等式的运用,考查学生分析解决问题的能力,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,2] | C. | (-∞,4) | D. | (-∞,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
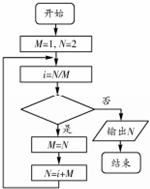 执行如图的程序框图,若输出的值为$\frac{35}{4}$,则判断框中可以填( )
执行如图的程序框图,若输出的值为$\frac{35}{4}$,则判断框中可以填( )| A. | i$>\frac{3}{2}$? | B. | i$≥\frac{3}{2}$? | C. | i>$\frac{5}{4}$? | D. | i$≥\frac{5}{4}$? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
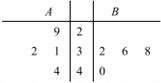 将某商场A,B两个品牌店在某日14:00-18:00四个时段(每个小时作为一个时段)的客流量统计并绘制成如图所示的茎叶图.
将某商场A,B两个品牌店在某日14:00-18:00四个时段(每个小时作为一个时段)的客流量统计并绘制成如图所示的茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x=2,y=1} | B. | $\left\{{\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.}\right\}$ | C. | {2,1} | D. | {(2,1)} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com