
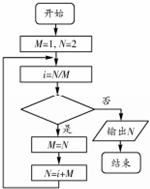
 执行如图的程序框图,若输出的值为$\frac{35}{4}$,则判断框中可以填( )
执行如图的程序框图,若输出的值为$\frac{35}{4}$,则判断框中可以填( )| A. | i$>\frac{3}{2}$? | B. | i$≥\frac{3}{2}$? | C. | i>$\frac{5}{4}$? | D. | i$≥\frac{5}{4}$? |
分析 模拟执行程序,依次写出每次循环得到的i,M,N的值,根据输出的值为$\frac{35}{4}$,即可得解判断框中的条件.
解答 解:模拟执行程序,可得
第一次,i=2,M=2,N=4;
第二次,i=2,M=4,N=6;
第三次,i=$\frac{3}{2}$,M=6,N=$\frac{15}{2}$;
第四次,i=$\frac{5}{4}$,M=$\frac{15}{2}$,N=$\frac{35}{4}$;
第五次,i=$\frac{7}{6}$,此时必须终止循环,观察可知判断框中可以填i$≥\frac{5}{4}$?,
故选:D.
点评 本题主要考查了算法与程序框图,意在考查学生的分析能力,属于基础题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
 已知P-ABC为正三棱锥,底面边长为2,设D为PB的中点,且AD⊥PC,如图所示
已知P-ABC为正三棱锥,底面边长为2,设D为PB的中点,且AD⊥PC,如图所示查看答案和解析>>
科目:高中数学 来源: 题型:填空题
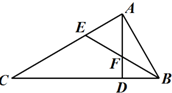 如图所示,在△ABC中,∠CAB=90°,AD⊥BC于D,BE是∠ABC的平分线,交AD于F,已知DF=$\sqrt{2}$,AF=$\sqrt{5}$,EC=2$\sqrt{5}$,则AE=2$\sqrt{2}$.
如图所示,在△ABC中,∠CAB=90°,AD⊥BC于D,BE是∠ABC的平分线,交AD于F,已知DF=$\sqrt{2}$,AF=$\sqrt{5}$,EC=2$\sqrt{5}$,则AE=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|1<x≤2} | C. | {x|1≤x≤2} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{13i}{5}$ | B. | -$\frac{13}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com