
分析 根据题意,利用正弦定理、三角形面积公式以及余弦定理,结合三角函数的有界性,即可求出m的取值范围.
解答 解:如图所示,
由正弦定理知,
$\frac{si{n}^{2}∠ABC+si{n}^{2}∠BCA+si{n}^{2}∠BAC}{sin∠ABC•sin∠BCA}$=$\frac{{b}^{2}{+c}^{2}{+a}^{2}}{bc}$,
由三角形面积公式可得$\frac{1}{2}$bcsin∠BAC=$\frac{1}{2}$a•AD,
又AD=a,
所以bcsin∠BAC=a2,
由余弦定理得b2+c2=a2+2bccos∠BAC,
故$\frac{{b}^{2}{+c}^{2}{+a}^{2}}{bc}$=2sin∠BAC+2cos∠BAC
=2$\sqrt{2}$sin(∠BAC+$\frac{π}{4}$)≤2$\sqrt{2}$,
所以m≥2$\sqrt{2}$,
即实数m的取值范围是[2$\sqrt{2}$,+∞).
故答案为:[2$\sqrt{2}$,+∞).
点评 本题考查了正弦定理、余弦定理、三角形面积公式的应用问题,也考查了综合运用知识的能力.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [1,3) | C. | [-1,1) | D. | (-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
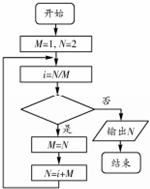 执行如图的程序框图,若输出的值为$\frac{35}{4}$,则判断框中可以填( )
执行如图的程序框图,若输出的值为$\frac{35}{4}$,则判断框中可以填( )| A. | i$>\frac{3}{2}$? | B. | i$≥\frac{3}{2}$? | C. | i>$\frac{5}{4}$? | D. | i$≥\frac{5}{4}$? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
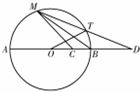 如图所示,直线DA过圆O的圆心,且交圆O于A,B两点,BC=CO=$\frac{1}{2}$BD,DM为圆O的一条割线,且与圆O交于M,T两点.
如图所示,直线DA过圆O的圆心,且交圆O于A,B两点,BC=CO=$\frac{1}{2}$BD,DM为圆O的一条割线,且与圆O交于M,T两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| P(X2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com