
设有一颗彗星沿一椭圆轨道绕地球运行,地球恰好位于椭圆轨道的焦点处,当此彗星离地球相距m万千米和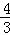 m万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为
m万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为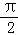 和
和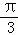 ,求该彗星与地球的最近距离.
,求该彗星与地球的最近距离.
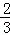 m万千米.
m万千米.
【解析】
试题分析:仔细分析题意,由椭圆的几何意义可知:只有当该彗星运行到椭圆的较近顶点处时,彗星与地球的距离才达到最小值即为a﹣c,这样把问题就转化为求a,c或a﹣c.
【解析】
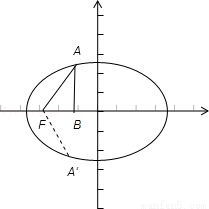
建立如图所示直角坐标系,设地球位于焦点F(﹣c,0)处,
椭圆的方程为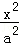 +
+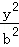 =1,
=1,
当过地球和彗星的直线与椭圆的长轴夹角为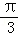 时,
时,
由椭圆的几何意义可知,彗星A只能满足∠xFA=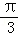 (或∠xFA′=
(或∠xFA′=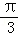 ).
).
作AB⊥Ox于B,则|FB|=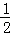 |FA|=
|FA|=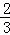 m,
m,
故由椭圆的第二定义可得
m=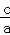 (
(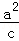 ﹣c),①
﹣c),①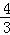 m=
m=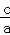 (
(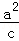 ﹣c+
﹣c+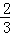 m).②
m).②
两式相减得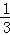 m=
m=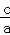 •
•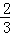 m,∴a=2c.
m,∴a=2c.
代入①,得m= (4c﹣c)=
(4c﹣c)=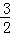 c,
c,
∴c=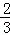 m.∴a﹣c=c=
m.∴a﹣c=c=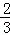 m.
m.
答:彗星与地球的最近距离为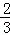 m万千米.
m万千米.


科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:解答题
某种产品每件成本为6元,每件售价为x元(x>6),年销量为u万件,若已知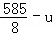 与
与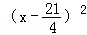 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润y关于x的函数关系式.
(2)求售价为多少时,年利润最大,并求出最大年利润.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.1 导数的概念练习卷(解析版) 题型:填空题
在曲线y=x2+1的图象上取一点(1,2)及附近一点(1+△x,2+△y),则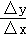 为 .
为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:解答题
某大桥在涨水时有最大跨度的中央桥孔如图所示,已知上部呈抛物线形,跨度为20 m,拱顶距水面6 m,桥墩高出水面4 m,现有一货船欲过此孔,该货船水下宽度不超过18 m,目前吃水线上部分中央船体高5 m,宽16 m,且该货船在现在状况下还可多装1000 t货物,但每多装150 t货物,船体吃水线就要上升0.04 m,若不考虑水下深度,该货船在现在状况下能否直接或设法通过该桥孔?为什么?
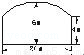
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:选择题
(4分)如图,花坛水池中央有一喷泉,水管OP=1m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面2m,P距抛物线对称轴1m,则在水池直径的下列可选值中,最合算的是( )

A.2.5m B.4m C.5m D.6m
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.3 抛物线练习卷(解析版) 题型:填空题
抛物线y=﹣ x2上的动点M到两定点F(0,﹣1),E(1,﹣3)的距离之和的最小值为 .
x2上的动点M到两定点F(0,﹣1),E(1,﹣3)的距离之和的最小值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷2(解析版) 题型:选择题
(2分)若角α、β的终边关于y轴对称,则α、β的关系一定是(其中k∈Z)( )
A.α+β=π B.α﹣β=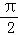 C.α﹣β=(2k+1)π D.α+β=(2k+1)π
C.α﹣β=(2k+1)π D.α+β=(2k+1)π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com