练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （4分）如图，花坛水池中央有一喷泉，水管OP=1m，水从喷头P喷出后呈抛物线状先向上至最高点后落下，若最高点距水面2m，P距抛物线对称轴1m，则在水池直径的下列可选值中，最合算的是（ ）

    A.2.5m B.4m C.5m D.6m

     

    5

    【解析】

    试题分析：建立直角坐标系，借助坐标法先求出落点的最远距离，从而估算出水池直径即可．

    【解析】
    以O为原点，OP所在直线为y轴建立直角坐标系（如图），则抛物线方程可设为

    y=a（x﹣1）2+2，P点坐标为（0，1），

    ∴1=a+2．∴a=﹣1．

    ∴y=﹣（x﹣1）2+2．

    令y=0，得（x﹣1）2=2，∴x=1±．

    ∴水池半径OM=+1≈2.414（m）．

    因此水池直径约为2×|OM|=4.828（m）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷（解析版） 题型：填空题

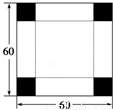
    如图，在边长为60cm的正方形铁皮的四角切去相等的正方形，再把它的边沿虚线折起，做成一个无盖的方底箱子，最大容积是 ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.1 导数的概念练习卷（解析版） 题型：解答题

    试求过点P（3，5）且与曲线y=x2相切的直线方程．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷（解析版） 题型：解答题

    （2003•上海）如图，某隧道设计为双向四车道，车道总宽22米，要求通行车辆限高4.5米，隧道全长2.5千米，隧道的拱线近似地看成半个椭圆形状．

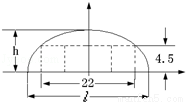
    （1）若最大拱高h为6米，则隧道设计的拱宽l是多少？

    （2）若最大拱高h不小于6米，则应如何设计拱高h和拱宽l，才能使半个椭圆形隧道的土方工程量最最小？（半个椭圆的面积公式为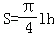，柱体体积为：底面积乘以高．本题结果精确到0.1米）

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷（解析版） 题型：解答题

    设有一颗彗星沿一椭圆轨道绕地球运行，地球恰好位于椭圆轨道的焦点处，当此彗星离地球相距m万千米和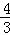m万千米时，经过地球和彗星的直线与椭圆的长轴夹角分别为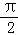和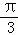，求该彗星与地球的最近距离．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.3 抛物线练习卷（解析版） 题型：解答题

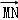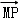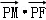    设F（1，0），点M在x轴上，点P在y轴上，且=2，=0；

    （1）当点P在y轴上运动时，求点N的轨迹C的方程；

    （2）设A（x1，y1），B（x2，y2），D（x3，y3）是曲线C上除去原点外的不同三点，且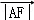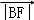，，成等差数列，当线段AD的垂直平分线与x轴交于点E（3，0）时，求点B的坐标．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.3 抛物线练习卷（解析版） 题型：选择题

    （2009•四川）已知直线l1：4x﹣3y+6=0和直线l2：x=﹣1，抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是（ ）

    A.2 B.3 C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.1 椭圆练习卷（解析版） 题型：解答题

    已知椭圆E的中心在坐标原点O，两个焦点分别为A（﹣1，0），B（1，0），一个顶点为H（2，0）．

    （1）求椭圆E的标准方程；

    （2）对于x轴上的点P（t，0），椭圆E上存在点M，使得MP⊥MH，求实数t的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷1（解析版） 题型：填空题

    （5分）（2007•江苏）某时钟的秒针端点A到中心点O的距离为5cm，秒针均匀地绕点O旋转，当时间t=0时，点A与钟面上标12的点B重合，将A，B两点的距离d（cm）表示成t（s）的函数，则d=　 　，其中t∈[0，60]．

     

    查看答案和解析>>

    同步练习册答案