
已知椭圆E的中心在坐标原点O,两个焦点分别为A(﹣1,0),B(1,0),一个顶点为H(2,0).
(1)求椭圆E的标准方程;
(2)对于x轴上的点P(t,0),椭圆E上存在点M,使得MP⊥MH,求实数t的取值范围.
(1) ;(2)(﹣2,﹣1).
;(2)(﹣2,﹣1).
【解析】
试题分析:(1)由两个焦点分别为A(﹣1,0),B(1,0),上顶点为D(2,0),得到椭圆的半长轴a,半焦距c,再求得半短轴b,
最后由椭圆的焦点在X轴上求得方程.
(2)利用向量垂直即可求得M点的横坐标x0,从而解决问题.
【解析】
(1)由题意得,c=1,a=2,则b=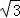
故所求的椭圆标准方程为 ;
;
(2)设M(x0,y0)(x0≠±2),则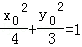 ①
①
又由P(t,0),H(2,0).则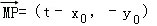 ,
,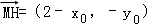
由MP⊥MH可得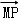
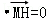 ,即(t﹣x0,﹣y0)•(2﹣x0,﹣y0)=
,即(t﹣x0,﹣y0)•(2﹣x0,﹣y0)=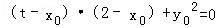
由①②消去y0,整理得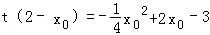 ②
②
∵x0≠2,∴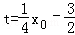
∵﹣2<x0<2,∴﹣2<t<﹣1
故实数t的取值范围为(﹣2,﹣1).


科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.2导数的运算练习卷(解析版) 题型:填空题
设函数 ,集合M={x|f(x)<0},P={x|f′(x)>0},若M⊆P,则实数a的取值范围是 .
,集合M={x|f(x)<0},P={x|f′(x)>0},若M⊆P,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:选择题
(4分)如图,花坛水池中央有一喷泉,水管OP=1m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面2m,P距抛物线对称轴1m,则在水池直径的下列可选值中,最合算的是( )

A.2.5m B.4m C.5m D.6m
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.1 椭圆练习卷(解析版) 题型:解答题
(2005•上海)点A、B分别是椭圆 +
+ =1长轴的左、右焦点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴上方,PA⊥PF.
=1长轴的左、右焦点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴上方,PA⊥PF.
(1)求P点的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,求椭圆上的点到点M的距离d的最小值.

查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.1 椭圆练习卷(解析版) 题型:选择题
(3分)(2013•韶关三模)椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
A.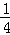 B.
B. C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 1.2 简单的逻辑联结词练习卷(解析版) 题型:解答题
(10分)已知命题p:x1和x2是方程x2﹣mx﹣2=0的两个实根,不等式a2﹣5a﹣3≥|x1﹣x2|对任意实数m∈[﹣1,1]恒成立;命题q:不等式ax2+2x﹣1>0有解,若命题p是真命题,命题q是假命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修三 7.5 空间直角坐标系练习卷(解析版) 题型:
若向量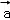 在y轴上的坐标为0,其他坐标不为0,那么与向量
在y轴上的坐标为0,其他坐标不为0,那么与向量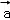 平行的坐标平面是( )
平行的坐标平面是( )
A.xOy平面 B.xOz平面 C.yOz平面 D.以上都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com