
| A. | -4 | B. | 4 | C. | $-\frac{27}{7}$ | D. | $\frac{27}{7}$ |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
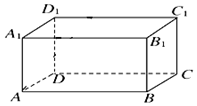 如图,长方体ABCD-A1B1C1D1中,AB=20,BC=13,AA1=12,过点A1D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.
如图,长方体ABCD-A1B1C1D1中,AB=20,BC=13,AA1=12,过点A1D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄ξ服从正态分布N(μ,σ2),同时随机抽取100位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分别区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.
京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄ξ服从正态分布N(μ,σ2),同时随机抽取100位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分别区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com