
分析 (1)不等式要恒成立,即要当x大于0时,t小于等于一个关系式,设这个关系式为一个函数h(x),求出h(x)的导函数,令导函数等于0求出x的值,利用x的值分区间讨论导函数的正负,得到函数h(x)的单调区间,根据函数的增减性得到h(x)的最小值,进而得到t的取值范围;
(2)求出F(x)的导函数,令导函数等于0,得到x+$\frac{1}{x}$等于一个关系式,设y=x+$\frac{1}{x}$,且x大于0小于2,画出该函数的图象,如图所示,然后分m=1,m大于$\frac{1}{2}$小于2,m大于0小于等于$\frac{1}{2}$和m大于等于2,四种情况,根据函数的图象,即可得到相应区间上极值点的个数.
解答 解:(1)若f(x)≥$\frac{t}{x}$-lnx (t为实数)恒成立,
因为x>0,
所以只需要t≤2xlnx在(0,+∞)恒成立即可,
令h(x)=2xlnx,则h′(x)=2(1+lnx),
当x∈(0,$\frac{1}{e}$)时,h′(x)<0,
所以h(x)在(0,$\frac{1}{e}$)上是减函数,
当x∈($\frac{1}{e}$,+∞)时,h′(x)>0,
所以h(x)在($\frac{1}{e}$,+∞)上是增函数,
所以h(x)min=h($\frac{1}{e}$)=-$\frac{2}{e}$,
所以t≤-$\frac{2}{e}$;
(2)由已知得F(x)=lnx+$\frac{{x}^{2}}{2}$-$\frac{{m}^{2}+1}{m}$x,
所以F′(x)=$\frac{1}{x}$+x-$\frac{{m}^{2}+1}{m}$,
令F′(x)=0,得到$\frac{1}{x}$+x=$\frac{{m}^{2}+1}{m}$,
令y=x+$\frac{1}{x}$,x∈(0,2),
画出该函数的图象,如图所示: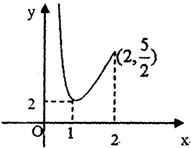
①当 $\frac{{m}^{2}+1}{m}$=2,即m=1时,F′(x)=0在区间(0,2)上只有一个根1,
此时F(x)在(0,2)上无极值点;
②当2<$\frac{{m}^{2}+1}{m}$<$\frac{5}{2}$,即$\frac{1}{2}$<m<2,且m≠1时,F′(x)=0在区间(0,2)上有两个不等根,
不妨设为x1,x2,且x1<x2,从图象上看在x1和x2两侧F′(x)都是异号的,
因此x1和x2都是F(x)的极值点,此时F(x)在(0,2)上有两个极值点;
③当 $\left\{\begin{array}{l}{0<m<2}\\{\frac{1}{m}≥2}\end{array}\right.$,即0<m≤$\frac{1}{2}$时,方程在区间(0,2)上只有一个根m,
由该方程所对应的二次函数图象可知,F′(x)在m两侧的符号不同,
因此函数F(x)在区间(0,2)上只有一个极值点;
④当 $\left\{\begin{array}{l}{0<\frac{1}{m}<2}\\{m≥2}\end{array}\right.$,即m≥2时,方程在区间(0,2)上只有一个根$\frac{1}{m}$,
由该方程所对应的二次函数图象可知,F′(x)在$\frac{1}{m}$两侧的符号不同,
因而函数F(x)在区间(0,2)上只有一个极值点,
综上,当m=1时,函数F(x)在区间(0,2)上无极值点;
当m∈(0,$\frac{1}{2}$)∪[2,+∞)时,函数F(x)在区间(0,2)上有一个极值点;
当m∈($\frac{1}{2}$,1)∪(1,2)时,函数F(x)在区间(0,2)上有两个极值点.
点评 此题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的极值,掌握导数在最大值、最小值问题中的应用,考查了分类讨论和数形结合的数学思想,是一道综合题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,8) | B. | (8,+∞) | C. | (0,$\frac{1}{8}$) | D. | ($\frac{1}{8}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
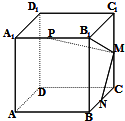 如图所示,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱CC1,BC,A1B1上的点,若∠B1MN=90°.则∠PMN的大小是( )
如图所示,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱CC1,BC,A1B1上的点,若∠B1MN=90°.则∠PMN的大小是( )| A. | 等于90° | B. | 小于90° | C. | 大于90° | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_5^5$ | B. | $A_3^3•A_3^3$ | C. | $\frac{A_5^5}{A_3^3}$ | D. | $A_3^3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 爱吃巧克力 | 不爱吃巧克力 | 合计 | |
| 数学成绩好 | 25 | 5 | 40 |
| 数学成绩一般 | 25 | 35 | 60 |
| 合计 | 50 | 50 | 100 |
| P(K2≥k) | 0.1 | 0.05 | 0.025 | 0.01 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | 至少有99%的把握认为“数学成绩好”与“爱吃巧克力”有关 | |
| B. | 至少有95%的把握认为“数学成绩好”与“爱吃巧克力”有关 | |
| C. | 至少有99%的把握认为“数学成绩好”与“爱吃巧克力”无关 | |
| D. | 至少有95%的把握认为“数学成绩好”与“爱吃巧克力”无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com