
分析 (1)f′(x)=2x-$\frac{a}{x}$-1,分情况讨论,即可求函数f(x)的单调区间;
(2)求出k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=(x2+x1)-$\frac{aln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-1=-2a-$\frac{1}{2}$,进而ln$\frac{1+\sqrt{1+8a}}{1-\sqrt{1+8a}}$=$\sqrt{1+8a}$,可得$\sqrt{1+8a}$=0,a=-$\frac{1}{8}$与a>-$\frac{1}{8}$矛盾,即可得出结论.
解答 解:(1)依题意知函数的定义域为(0,+∞),
f′(x)=2x-$\frac{a}{x}$-1=$\frac{2{x}^{2}-x-a}{x}$,
t=2x2-x-a,△=1+8a≤0,a≤-$\frac{1}{8}$,f′(x)≥0,f(x)的单调递增区间为(0,+∞);
当a>-$\frac{1}{8}$时,令f′(x)>0,得0<x<$\frac{1-\sqrt{1+8a}}{4}$或x>$\frac{1+\sqrt{1+8a}}{4}$,故函数f(x)的单调递增区间为(0,$\frac{1-\sqrt{1+8a}}{4}$),($\frac{1+\sqrt{1+8a}}{4}$,+∞);
令f′(x)<0,得0<x<$\frac{1+\sqrt{1+8a}}{4}$,故函数f(x)的单调递减区间为($\frac{1-\sqrt{1+8a}}{4}$,$\frac{1+\sqrt{1+8a}}{4}$).
(2)∵f(x)有两个极值点x1,x2,
∴x2+x1=$\frac{1}{2}$,x2x1=-$\frac{a}{2}$,x1=$\frac{1-\sqrt{1+8a}}{4}$,x2=$\frac{1+\sqrt{1+8a}}{4}$
∵k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=(x2+x1)-$\frac{aln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-1=-2a-$\frac{1}{2}$,
∴$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$=2,
∴ln$\frac{1+\sqrt{1+8a}}{1-\sqrt{1+8a}}$=$\sqrt{1+8a}$,
设t=$\sqrt{1+8a}$,则y=ln$\frac{1+t}{1-t}$-t,
∴y′=$\frac{2}{1-{t}^{2}}$-1=$\frac{1+{t}^{2}}{1-{t}^{2}}$>0,
∴函数在(-1,1)上单调递增,
∴$\sqrt{1+8a}$=0,a=-$\frac{1}{8}$与a>-$\frac{1}{8}$矛盾,
故不存在.
点评 本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力,分类讨论等综合解题能力,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
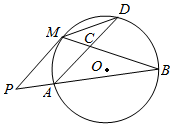 如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则MD等于( )
如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则MD等于( )| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{9}{4}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
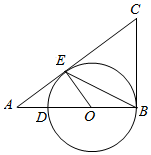 如图,E为⊙O上一点,点A在直径BD的延长线上,过点B作⊙O的切线交AE的延长线于点C,CE=CB.
如图,E为⊙O上一点,点A在直径BD的延长线上,过点B作⊙O的切线交AE的延长线于点C,CE=CB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com