
分析 求出函数的导数,根据函数的单调性求出函数的解析式,从而求出函数的值域即可.
解答 解:∵y=x3+bx2+cx,∴y′=3x2+2bx+c,
若函数在区间(-∞,0)及[2,+∞)是增函数,在(0,2)是减函数,
则0,2是方程3x2+2bx+c=0的根,
∴$\left\{\begin{array}{l}{c=0}\\{12+4b+c=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=-3}\\{c=0}\end{array}\right.$,
∴y=x3-3x2,
函数在[-1,0)递增,在(0,2)递减,在(2,4]递增,
而f(-1)=-4,f(0)=0,f(2)=-4,f(4)=16,
故此函数的值域是[-4,16].
点评 本题考查了函数的单调性、最值、极值问题,考查导数的应用,是一道基础题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,且$\frac{AE}{EB}$=$\frac{CF}{FB}$=2,将此正方形沿DE,DF折起,使点A,C重合于点P,若O为线段EF任一点,DO与平面PEF所成的角为θ,则tanθ的最大值是$\frac{3\sqrt{14}}{7}$.
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,且$\frac{AE}{EB}$=$\frac{CF}{FB}$=2,将此正方形沿DE,DF折起,使点A,C重合于点P,若O为线段EF任一点,DO与平面PEF所成的角为θ,则tanθ的最大值是$\frac{3\sqrt{14}}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 倾向“平面几何选讲” | 倾向“坐标系与参数方程” | 倾向“不等式选讲” | 合计 | |
| 男生 | 16 | 4 | 6 | 26 |
| 女生 | 4 | 8 | 12 | 24 |
| 合计 | 20 | 12 | 18 | 50 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
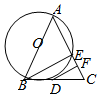 已知:AB为圆O的直径,AB=AC,AC,BC分别交圆O于E,D,连接BE,DF⊥AC于F
已知:AB为圆O的直径,AB=AC,AC,BC分别交圆O于E,D,连接BE,DF⊥AC于F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
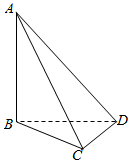 如图,在三棱锥A-BCD中,三条棱AB、BC、CD两两垂直,且AD与平面BCD成45°角,与平面ABC成30°角.
如图,在三棱锥A-BCD中,三条棱AB、BC、CD两两垂直,且AD与平面BCD成45°角,与平面ABC成30°角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图在底面为正方形,侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图在底面为正方形,侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com