
 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,且$\frac{AE}{EB}$=$\frac{CF}{FB}$=2,将此正方形沿DE,DF折起,使点A,C重合于点P,若O为线段EF任一点,DO与平面PEF所成的角为θ,则tanθ的最大值是$\frac{3\sqrt{14}}{7}$.
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,且$\frac{AE}{EB}$=$\frac{CF}{FB}$=2,将此正方形沿DE,DF折起,使点A,C重合于点P,若O为线段EF任一点,DO与平面PEF所成的角为θ,则tanθ的最大值是$\frac{3\sqrt{14}}{7}$. 分析 根据条件作出折叠后对应的图形,得到∠DOP是OD与底面EFP所成的角,根据DP的定值,则tanθ的最大值等价为OP最小,结合三角形的边角关系进行求解即可.
解答 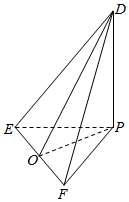 解:∵正方形ABCD的边长为3,$\frac{AE}{EB}$=$\frac{CF}{FB}$=2,
解:∵正方形ABCD的边长为3,$\frac{AE}{EB}$=$\frac{CF}{FB}$=2,
∴AE=CF=2,BE=BF=1,
则EF=$\sqrt{2}$,折叠后对应的图形如图,
则此时EP=FP=AE=2,
∵CD⊥CF,DA⊥AE,
∴折叠后,PD⊥PF,DP⊥PE,
即PD⊥平面EFP,
则∠DOP是OD与底面EFP所成的角,且DP=3,
则tanθ=tan∠DOP=$\frac{DP}{OP}$=$\frac{3}{OP}$,
则要使tanθ最大,则只要OP最小即可,此时OP⊥EF,
即O是EF的中点,
则OE=$\frac{1}{2}$EF=$\frac{\sqrt{2}}{2}$,OP=$\sqrt{P{E}^{2}-O{E}^{2}}$=$\sqrt{{2}^{2}-(\frac{\sqrt{2}}{2})^{2}}=\sqrt{4-\frac{2}{4}}$=$\sqrt{\frac{14}{4}}$=$\frac{\sqrt{14}}{2}$,
则tanθ的最小值为tanθ=$\frac{3}{\frac{\sqrt{14}}{2}}$=$\frac{6}{\sqrt{14}}$=$\frac{3\sqrt{14}}{7}$,
故答案为:$\frac{3\sqrt{14}}{7}$
点评 本题主要考查线面角的计算以及三角函数的最值问题,根据条件作出折叠后的图形,找出线面角,进行转化是解决本题的关键.综合性较强,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{2}$ | B. | $\frac{49}{2}$ | C. | 12 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com