
���� �ٶ���[x]Ϊ������x������������Ӷ��ɵ�0��|$\frac{1}{[\frac{1}{?}]+2}$-0|��?���Ӷ�ȷ��0Ϊ���������ġ��۵㡱��
����cos$\frac{��}{2}$��cos$\frac{��}{3}$��cos$\frac{��}{4}$��cos$\frac{��}{5}$������cos$\frac{��}{n+1}$�ɵ�0���Ǽ���{cos$\frac{��}{n+1}$|n��N*}�ġ��۵㡱��
����sinx��x��x�ʣ�0��1��֪������?��0��0��|sin?|��?���Ӷ�ȷ����
����$\frac{1}{2}$��$\frac{2}{3}$��$\frac{3}{4}$������$\frac{n}{n+1}$֪0���Ǽ���{$\frac{n}{n+1}$|n��N*}�ġ��۵㡱��
��� �⣺�ٶ���[x]Ϊ������x�����������
�������?��0��$\frac{1}{?}$��$[\frac{1}{?}]$+2��
��?��$\frac{1}{[\frac{1}{?}]+2}$��
ȡ������x=$\frac{1}{[\frac{1}{?}]+2}$���ɵã�
0��|$\frac{1}{[\frac{1}{?}]+2}$-0|��?��
��0Ϊ���������ġ��۵㡱��
��{cos$\frac{��}{n+1}$|n��N*}�е�Ԫ�أ�
cos$\frac{��}{2}$��cos$\frac{��}{3}$��cos$\frac{��}{4}$��cos$\frac{��}{5}$������cos$\frac{��}{n+1}$��
��0��$\frac{1}{2}$��$\frac{\sqrt{2}}{2}$��cos$\frac{��}{5}$������cos$\frac{��}{n+1}$��
��0���Ǽ���{cos$\frac{��}{n+1}$|n��N*}�ġ��۵㡱��
�ۡ�sinx��x��x�ʣ�0��1����
�������?��0��0��|sin?|��?��
��0Ϊ����{sin$\frac{��}{n+1}$|n��N*}�ġ��۵㡱��
�ܡ�$\frac{1}{2}$��$\frac{2}{3}$��$\frac{3}{4}$������$\frac{n}{n+1}$��
��0���Ǽ���{$\frac{n}{n+1}$|n��N*}�ġ��۵㡱��
�ʴ�Ϊ���٢ۣ�
���� ���⿼����ѧ�����¶���Ľ���������Ӧ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 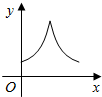 | B�� | 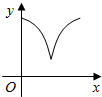 | C�� | 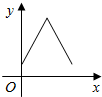 | D�� | 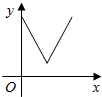 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| X | 200 | 300 | 400 | 500 |
| P | 0.20 | 0.35 | 0.30 | 0.15 |
| A�� | 706Ԫ | B�� | 690Ԫ | C�� | 754Ԫ | D�� | 720Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{1��\frac{��}{4}}��$ | B�� | $��{\frac{1}{2}��\frac{��}{4}}��$ | C�� | $��{\sqrt{2}��\frac{��}{4}}��$ | D�� | $��{2��\frac{��}{4}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com