
分析 本题属于利用导数求曲线上某点处的切线方程,属于基础题型.首先求出f'(x)后,切线方程与直线y=-x平行,从而令 $-\frac{1}{{e}^{x}}=-1$,可求出切点.
解答 解:对函数f(x)=$\frac{1}{e^x}$求导:
$f'(x)=-\frac{1}{{e}^{x}}$;
∵函数f(x)与直线y=-x平行;
∴$-\frac{1}{{e}^{x}}=-1$;
∴x=0;
从而得到当x=0时,则f(0)=1;
点(0,1)满足f(x)曲线方程,则切线方程为:y-f(0)=-1×$\$ (x-0)⇒x+y-1=0
故答案为:x+y-1=0
点评 本题属于利用导数求曲线上某点处的切线方程,属于基础题型,也是高考常考题型之一,考生应当熟练掌握.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
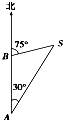 (文)如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8$\sqrt{2}$ n mile.求此船的航速.
(文)如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8$\sqrt{2}$ n mile.求此船的航速.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 不是充分条件,也不是必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 真,假,真 | B. | 假,假,真 | C. | 真,真,假 | D. | 假,假,假 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 | … |
| f(x) | 5 | 1 | 3 | 2 | 6 | 4 | … |
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com