
已知函数 ,其中
,其中 为实数,常数
为实数,常数 .
.
(1) 若 是函数
是函数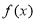 的一个极值点,求
的一个极值点,求 的值;
的值;
(2) 当 取正实数时,求函数
取正实数时,求函数 的单调区间;
的单调区间;
(3) 当 时,直接写出函数
时,直接写出函数 的所有减区间.
的所有减区间.
(1)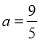 ;(2)当
;(2)当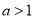 时,
时,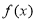 的单调递增区间为
的单调递增区间为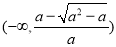 ,
,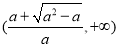 ,
,
单调减区间为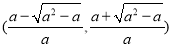 ;当
;当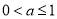 时,
时, 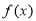 的单调增区间是
的单调增区间是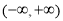 ;(3)单调减区间是
;(3)单调减区间是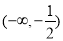 ,
,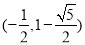 ,
,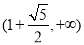 .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的极值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先对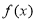 求导,由于
求导,由于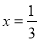 是函数
是函数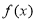 的一个极值点,所以
的一个极值点,所以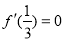 ,解出a的值,需验证,当
,解出a的值,需验证,当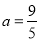 时,
时,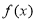 是否有极值点;第二问,对
是否有极值点;第二问,对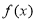 求导,通过对判别式的讨论确定
求导,通过对判别式的讨论确定 有几个根,再数形结合判断函数
有几个根,再数形结合判断函数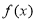 的单调区间;第三问,把
的单调区间;第三问,把 代入,对
代入,对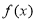 求导,令
求导,令 ,解不等式,解出减区间即可.
,解不等式,解出减区间即可.
试题解析:(1)【解析】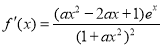 (2分)
(2分)
因为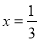 是函数
是函数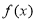 的一个极值点,所以
的一个极值点,所以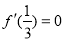 ,
,
即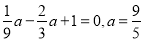 .
.
而当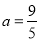 时,
时,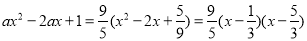 ,
,
可验证: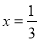 是函数
是函数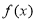 的一个极值点.因此
的一个极值点.因此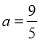 . (4分)
. (4分)
(2) 当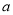 取正实数时,
取正实数时,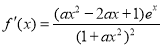 ,
,
令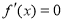 得
得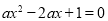 ,
,
当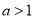 时,解得
时,解得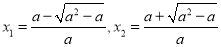 .
.
所以当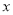 变化时,
变化时,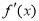 、
、 的变化是
的变化是
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
所以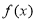 的单调递增区间为
的单调递增区间为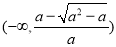 ,
,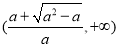 ,
,
单调减区间为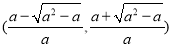 ;
;
当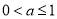 时,
时,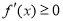 恒成立,故
恒成立,故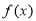 的单调增区间是
的单调增区间是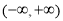 . (9分)
. (9分)
(3) 当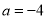 时,
时, 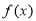 的单调减区间是
的单调减区间是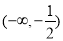 ,
,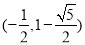 ,
,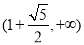 .(12分)
.(12分)
考点:导数的运算、利用导数判断函数的单调性、利用导数求函数的极值.


科目:高中数学 来源:2015届四川成都树德中学高二3月月考文科数学试卷(解析版) 题型:选择题
已知圆 ,点
,点 是圆
是圆 内的一点,过点
内的一点,过点 的圆
的圆 的最短弦在直线
的最短弦在直线 上,直线
上,直线 的方程为
的方程为 ,那么( )
,那么( )
A. 且
且 与圆
与圆 相交 B.
相交 B. 且
且 与圆
与圆 相切
相切
C. 且
且 与圆
与圆 相离 D.
相离 D. 且
且 与圆
与圆 相离
相离
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试理科数学试卷(解析版) 题型:选择题
已知定义在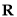 上的函数
上的函数 满足①
满足① ,②
,② ,③在
,③在 上表达式为
上表达式为 ,则函数
,则函数 与函数
与函数 的图像在区间
的图像在区间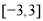 上的交点个数为( )
上的交点个数为( )
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试理科数学试卷(解析版) 题型:选择题
已知 、
、 取值如下表:
取值如下表:
| 0 | 1 | 4 | 5 | 6 |
| 1.3 |
|
| 5.6 | 7.4 |
画散点图分析可知: 与
与 线性相关,且求得回归方程为
线性相关,且求得回归方程为 ,则
,则 的值(精确到0.1)为( )
的值(精确到0.1)为( )
A.1.5 B.1.6 C.1.7 D.1.8
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试文科数学试卷(解析版) 题型:解答题
已知等比数列 的各项均为正数,且
的各项均为正数,且 ,
, .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,则输出的结果是( )
A.14 B.15 C.16 D.17

查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数 在
在 上为增函数,
上为增函数, ,
,
(1)求 的值;
的值;
(2)当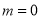 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;
(3)若在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com