
分析 由题意可得直线y=x和直线y=2有交点,且y=x2+4x+2的图象和直线y=x有两个交点,即必须使函数y=2-x有零点,并且函数y=x2+3x+2=(x+1)(x+2)有两个零点,从而得到m的范围.
解答 解:由题意可得函数f(x)=$\left\{\begin{array}{l}{2,x>m}\\{{x}^{2}+4x+2,x≤m}\end{array}\right.$若它的图象和直线y=x有3个不同的交点,
即直线y=x和直线y=2有交点,且y=x2+4x+2的图象和直线y=x有两个交点,
即必须使函数y=2-x有零点,并且函数y=x2+3x+2=(x+1)(x+2)有两个零点,从而得到m<2并且m≥-1,
故答案为:[-1,2).
点评 本题主要考查函数零点与方程根的关系,体现了转化的数学思想,属于基础题.


科目:高中数学 来源: 题型:解答题
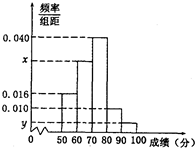 学校达标运动会后,为了解学生的体质情况,从中抽取了部分学生的成绩,得到一个容量为n的样本,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了如图的频率分布直方图,已知[50,60)与[90,100]两组的频数分别为24与6.
学校达标运动会后,为了解学生的体质情况,从中抽取了部分学生的成绩,得到一个容量为n的样本,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了如图的频率分布直方图,已知[50,60)与[90,100]两组的频数分别为24与6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有95%以上的把握认为“吸烟与患肺病有关” | |
| B. | 有95%以上的把握认为“吸烟与患肺病无关” | |
| C. | 有99%以上的把握认为“吸烟与患肺病有关” | |
| D. | 有99%以上的把握认为“吸烟与患肺病无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥A-BCDE中,∠ABC=30°,AB⊥AC,AF⊥BC,垂足为F,BE⊥平面ABC,CD∥BE,BC=4,BE=3,CD=1.
如图,在四棱锥A-BCDE中,∠ABC=30°,AB⊥AC,AF⊥BC,垂足为F,BE⊥平面ABC,CD∥BE,BC=4,BE=3,CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
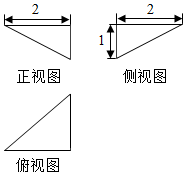
| A. | 2$\sqrt{2}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com