
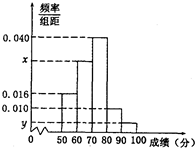
 ѧУ����˶����Ϊ�˽�ѧ����������������г�ȡ�˲���ѧ���ijɼ����õ�һ������Ϊn������������[50��60����[60��70����[70��80����[80��90����[90��100]�ķ�����������ͼ��Ƶ�ʷֲ�ֱ��ͼ����֪[50��60����[90��100]�����Ƶ���ֱ�Ϊ24��6��
ѧУ����˶����Ϊ�˽�ѧ����������������г�ȡ�˲���ѧ���ijɼ����õ�һ������Ϊn������������[50��60����[60��70����[70��80����[80��90����[90��100]�ķ�����������ͼ��Ƶ�ʷֲ�ֱ��ͼ����֪[50��60����[90��100]�����Ƶ���ֱ�Ϊ24��6������ ��1���������������������n��x��y��ֵ��
��2������Ƶ�ʷֲ�ֱ��ͼ�ܹ���ѧ���ɼ�����λ����ѧ���ɼ���ƽ������
��3����2�������ֱ�Ϊa1��a2��4��Ů���ֱ�Ϊb1��b2��b3��b4��������һ�������Ķ����¼�Ϊ�鵽2��Ů�����ɴ����ö����¼������2��ѧ����������1��������Ƶ�ʣ�
��� �⣺��1��������֪��������n=$\frac{24}{0.016��10}$=150��y=$\frac{6}{150��10}$=0.004��
x=0.1-0.004-0.010-0.016-0.040=0.030��
��2������ѧ���ɼ�����λ��m=70+$\frac{0.004}{0.04}$��10=71��
����ѧ���ɼ���ƽ����$\overline{x}$=55��0.16+65��0.30+75��0.40+85��0.10+95��0.04=70.6��
��3����2�������ֱ�Ϊa1��a2��4��Ů���ֱ�Ϊb1��b2��b3��b4��
��ȡ����ѧ���Ľ���У�
�����¼�����n=${C}_{6}^{2}$=15��
����������һ�������Ķ����¼�Ϊ�鵽2��Ů����
��2��ѧ����������1��������Ƶ��p=1-$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{3}{5}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע������¼����ʼ��㹫ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8�� | B�� | 16�� | C�� | 24�� | D�� | 32�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{3}{5}$ | B�� | -$\frac{6}{11}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{6}{11}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
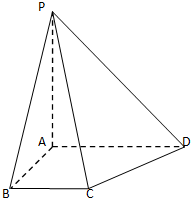 ������P-ABCD�У�ֱ��AP��AB��AD�������ֱ����AD��BC��AP=AB=AD=2BC��
������P-ABCD�У�ֱ��AP��AB��AD�������ֱ����AD��BC��AP=AB=AD=2BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com