
分析 (1)由已知利用余弦定理即可得解c的值.
(2)利用三角函数恒等变换的应用化简可得f(A)=sin(2A+$\frac{π}{6}$)-$\frac{1}{2}$,利用正弦函数的性质可求f(A)的最大值,利用正弦定理进而可求得此时△ABC的外接圆半径.
解答 (本题满分为12分)
解:(1)∵b2=a2+c2-2accosB,a=3,b=$\sqrt{7}$,$B=\frac{π}{3}$,
∴7=9+c2-2×$3×c×\frac{1}{2}$,整理可得:c2-3c+2=0,
解得:c=1或2…4分
(2)由二倍角公式得f(A)=$\frac{\sqrt{3}}{2}$sin2A+$\frac{1}{2}$cos2A-$\frac{1}{2}$,
∴f(A)=sin(2A+$\frac{π}{6}$)-$\frac{1}{2}$,
∴当A=$\frac{π}{6}$时,f(A)最大值为$\frac{1}{2}$,
此时△ABC为直角三角形,
此时△ABC的外接圆半径:$r=\frac{1}{2}×\frac{a}{sinA}=\frac{{\sqrt{7}}}{{2×\frac{1}{2}}}=\sqrt{7}$…12分
点评 本题主要考查了余弦定理,三角函数恒等变换的应用,正弦函数的性质,正弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
 已知某几何体的正(主)视图,侧(左)视图和俯视图均为边长为1的正方形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )
已知某几何体的正(主)视图,侧(左)视图和俯视图均为边长为1的正方形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
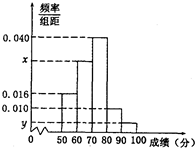 学校达标运动会后,为了解学生的体质情况,从中抽取了部分学生的成绩,得到一个容量为n的样本,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了如图的频率分布直方图,已知[50,60)与[90,100]两组的频数分别为24与6.
学校达标运动会后,为了解学生的体质情况,从中抽取了部分学生的成绩,得到一个容量为n的样本,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了如图的频率分布直方图,已知[50,60)与[90,100]两组的频数分别为24与6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有95%以上的把握认为“吸烟与患肺病有关” | |
| B. | 有95%以上的把握认为“吸烟与患肺病无关” | |
| C. | 有99%以上的把握认为“吸烟与患肺病有关” | |
| D. | 有99%以上的把握认为“吸烟与患肺病无关” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com