
分析 ①由f(|-x|)=f(|x|),即可得出f(|x|)为偶函数;
②若f(a)=|f(b)|其中a>0,b>0,∵a≠b,可得f(a)=|f(b)|=-f(b),利用对数的运算性质可得:log${\;}_{\frac{1}{2}}$(ab)=0,可得ab=1.
③函数f(-x2+2x)=$lo{g}_{\frac{1}{2}}[-(x-1)^{2}+1]$,由-x2+2x>0,解出可得函数的定义域为(0,2),即可判断出正误;
④由0<a<1,可得1+a>1-a,f(1+a)<0<f(1-a),作差|f(1-a)|-|f(1-a)|=-f(1+a)-f(1-a),化简即可得出正误.
解答 解:f(x)=log${\;}_{\frac{1}{2}}$x,x>0.
①函数f(|x|)=log${\;}_{\frac{1}{2}}$|x|,∵f(|-x|)=f(|x|),∴f(|x|)为偶函数,正确;
②若f(a)=|f(b)|其中a>0,b>0,∵a≠b,∴f(a)=|f(b)|=-f(b),
∴log${\;}_{\frac{1}{2}}$a+log${\;}_{\frac{1}{2}}$b=log${\;}_{\frac{1}{2}}$(ab)=0,∴ab=1.因此正确.
③函数f(-x2+2x)=$lo{g}_{\frac{1}{2}}(-{x}^{2}+2x)$=$lo{g}_{\frac{1}{2}}[-(x-1)^{2}+1]$,由-x2+2x>0,解得0<x<2,
∴函数的定义域为(0,2),因此在(1,3)上不具有单调性,不正确;
④若0<a<1,∴1+a>1-a,∴f(1+a)<0<f(1-a),故|f(1-a)|-|f(1-a)|=-f(1+a)-f(1-a)=-$lo{g}_{\frac{1}{2}}(1-{a}^{2})$<0,即|f(1-a)|<|f(1-a)|,因此正确.
综上可得:只有①②④正确.
故答案为:①②④.
点评 本题考查了对数函数的奇偶性、单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{21}{44}$ | B. | $\frac{15}{22}$ | C. | $\frac{21}{50}$ | D. | $\frac{9}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知某几何体的正(主)视图,侧(左)视图和俯视图均为边长为1的正方形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )
已知某几何体的正(主)视图,侧(左)视图和俯视图均为边长为1的正方形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
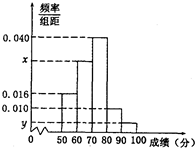 学校达标运动会后,为了解学生的体质情况,从中抽取了部分学生的成绩,得到一个容量为n的样本,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了如图的频率分布直方图,已知[50,60)与[90,100]两组的频数分别为24与6.
学校达标运动会后,为了解学生的体质情况,从中抽取了部分学生的成绩,得到一个容量为n的样本,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了如图的频率分布直方图,已知[50,60)与[90,100]两组的频数分别为24与6.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有95%以上的把握认为“吸烟与患肺病有关” | |
| B. | 有95%以上的把握认为“吸烟与患肺病无关” | |
| C. | 有99%以上的把握认为“吸烟与患肺病有关” | |
| D. | 有99%以上的把握认为“吸烟与患肺病无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥A-BCDE中,∠ABC=30°,AB⊥AC,AF⊥BC,垂足为F,BE⊥平面ABC,CD∥BE,BC=4,BE=3,CD=1.
如图,在四棱锥A-BCDE中,∠ABC=30°,AB⊥AC,AF⊥BC,垂足为F,BE⊥平面ABC,CD∥BE,BC=4,BE=3,CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
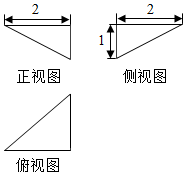
| A. | 2$\sqrt{2}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
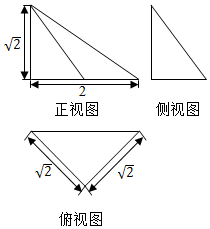
| A. | 2$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2+2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com