
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
分析 由已知中函数f(x)对于任意实数x满足条件f(x+2)=-$\frac{1}{f(x)}$,可确定函数f(x)是以4为周期的周期函数,进而根据周期函数的性质,从内到外依次去掉括号,即可得到答案.
解答 解:∵函数f(x)对于任意实数x满足条件f(x+2)=-$\frac{1}{f(x)}$,∴f(x+4)=f[(x+2)+2]=-$\frac{1}{f(x+2)}$=$\frac{1}{\frac{1}{f(x)}}$=f(x),
即函数f(x)是以4为周期的周期函数,
∵f(2)=-4,则f(f(6))=f[f(2)]=f(-4)=f(0)=-$\frac{1}{f(2)}$=$\frac{1}{4}$.
故选:C.
点评 本题考查的知识点是函数的周期性,函数的值,其中根据已知中函数f(x)对于任意实数x满足条件f(x+2)=-$\frac{1}{f(x)}$,判断出函数f(x)是以4为周期的周期函数,是解答本题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
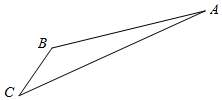 如图,旅客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从A乘缆车到B,再从B匀速步行到C.假设缆车匀速直线运动的速度为130米/分钟,山路AC长1260米,经测量,cosA=$\frac{12}{13}$,cosC=$\frac{3}{5}$.
如图,旅客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从A乘缆车到B,再从B匀速步行到C.假设缆车匀速直线运动的速度为130米/分钟,山路AC长1260米,经测量,cosA=$\frac{12}{13}$,cosC=$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 3$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到抛物线C的准线的距离的最小值为( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到抛物线C的准线的距离的最小值为( )| A. | $\frac{3}{2}$p | B. | 2p | C. | $\frac{5}{2}$p | D. | 3p |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com