
分析 (1)通过焦点F2(c,0),右准线l2:$x=\frac{a^2}{c}$,得到a,c关系,然后求解离心率.
(2)由(1)知$e=\frac{c}{a}=\frac{{\sqrt{3}}}{3}$,求出b2=2c2,设椭圆方程为2x2+3y2=6c2.设直线l的方程为$x=my-\sqrt{3}$,联立方程组,利用判别式以及韦达定理,求解三角形的面积,利用基本不等式求解面积的最大值,然后求解椭圆方程.
解答 解:(1)焦点F2(c,0),右准线l2:$x=\frac{a^2}{c}$,由题知|AB|=3|F1F2|,
即$2\frac{a^2}{c}=3•2c$,即a2=3c2,解得$e=\frac{c}{a}=\frac{{\sqrt{3}}}{3}$.
(2)由(1)知$e=\frac{c}{a}=\frac{{\sqrt{3}}}{3}$,得a2=3c2,b2=2c2,可设椭圆方程为2x2+3y2=6c2.
设直线l的方程为$x=my-\sqrt{3}$,代入椭圆的方程有,$(2{m^2}+3){y^2}-4\sqrt{3}y+6-6{c^2}=0$,
因为直线与椭圆相交,所以△=48m2-4(2m2+3)(6-6c2)>0,
由韦达定理得${y_1}+{y_2}=\frac{{4\sqrt{3}m}}{{2{m^2}+3}}$,${y_1}{y_2}=\frac{{6-6{c^2}}}{{2{m^2}+3}}$,又$\overrightarrow{DP}=2\overrightarrow{QD}$,所以y1=-2y2,
得到${y_1}=\frac{{8\sqrt{3}m}}{{2{m^2}+3}}$,${y_2}=\frac{{-4\sqrt{3}m}}{{2{m^2}+3}}$,${y_1}{y_2}=\frac{{6-6{c^2}}}{{2{m^2}+3}}=\frac{{-96{m^2}}}{{{{(2{m^2}+3)}^2}}}$,得到$1-{c^2}=-\frac{{16{m^2}}}{{2{m^2}+3}}$,
所以${S_{△DPQ}}=\frac{1}{2}|OD|•|{y_1}-{y_2}|=\frac{{\sqrt{3}}}{2}•|\frac{{12\sqrt{3}m}}{{2{m^2}+3}}|=18•\frac{|m|}{{2|m{|^2}+3}}=18•\frac{1}{{2|m|+\frac{3}{|m|}}}≤\frac{{3\sqrt{6}}}{2}$,
当且仅当${m^2}=\frac{3}{2}$时,等号成立,此时c2=5,代入△满足△>0,
所以所求椭圆方程为$\frac{x^2}{15}+\frac{y^2}{10}=1$.
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | r的取值范围是(-∞,+∞) | B. | r越大两个变童的相关程度越高 | ||
| C. | r,b符号相同 | D. | r,b符号相反 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 135° | C. | 60° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
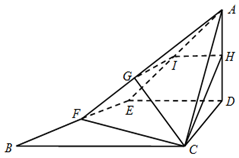 △ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点
△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | ||
| C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1或$\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1或$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{3}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com