
分析 若p∨q为真命题,p∧q为假命题,则p,q一真一假,进而可得实数m的取值范围.
解答 解:如果p为真命题,则有$\frac{m}{2}>m-1>0$,即1<m<2;
若果q为真命题,则64m2-32(7m-6)≥0,解得m≤$\frac{3}{2}$或m≥2.
因为p∨q为真命题,p∧q为假命题,所以p和q一真一假,
若p真q假,则$\frac{3}{2}$<m<2,
若p假q真,则m≤1或m≥2.
所以实数m的取值范围为(∞,1]∪($\frac{3}{2}$,+∞).
点评 本题以命题的真假判断与应用为载体,考查了直线与圆的位置关系,三角函数的图象和性质,复合命题等知识点,难度中档.


科目:高中数学 来源: 题型:选择题
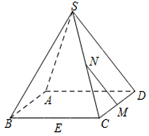 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:| A. | ①③ | B. | ③④ | C. | ①② | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
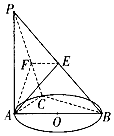 如图所示,PA垂直于圆O所在平面,AB是圆O的直径,C是圆O上一点,点A在PB,PC上的射影分别为E,F,则以下结论错误的是( )
如图所示,PA垂直于圆O所在平面,AB是圆O的直径,C是圆O上一点,点A在PB,PC上的射影分别为E,F,则以下结论错误的是( )| A. | PB⊥AF | B. | PB⊥EF | C. | AF⊥BC | D. | AE⊥BC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4033 | B. | -4033 | C. | 8066 | D. | -8066 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 |
| p | $\frac{1}{3}$ | a | $\frac{1}{6}$ |
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $2a+\frac{5}{6}$ | D. | $\frac{11}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com