
| A. | $y=\sqrt{3}x$ | B. | $y=-\sqrt{3}x$ | C. | y=2x | D. | y=-2x |
分析 由已知得圆心坐标为(0,4),半径长为2.因为直线斜率存在.设直线方程为 y=kx,根据圆心到直线的距离等于半径,确定k的值,从而求出直线方程
解答 解:圆心坐标为(0,4),半径长为2.
由直线过原点,当直线斜率不存在时,不合题意,
设直线方程为;y=kx,即kx-y=0.
则圆心到直线的距离d=$\frac{4}{\sqrt{1+{k}^{2}}}$=r=2
化简得:k2=3
又∵切点在第二象限,∴$k=-\sqrt{3}$
∴直线方程为;y=-$\sqrt{3}$x
故选:B.
点评 本题考查直线与圆相切时所满足的条件,灵活运用点到直线的距离公式化简求值,考查了数形结合的数学思想,是一道中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
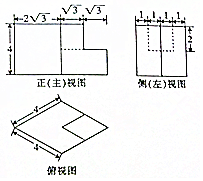
| A. | 64+18$\sqrt{3}$ | B. | 64+16$\sqrt{3}$ | C. | 96 | D. | 92-2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(6)<f(-7)<f(\frac{11}{2})$ | B. | $f(6)<f(\frac{11}{2})<f(-7)$ | C. | $f(-7)<f(\frac{11}{2})<f(6)$ | D. | $f(\frac{11}{2})<f(-7)<f(6)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
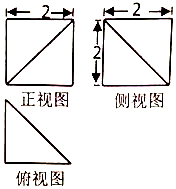
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com