
分析 (Ⅰ)由题意b=1,利用椭圆的离心率即可求得a的值,求得椭圆方程;
(Ⅱ)设直线MN的方程为y=k(x-1),代入椭圆方程,利用韦达定理及向量的坐标运算,即可证明λ+μ=0为定值.
解答 解:(Ⅰ)由点B(0,1)在椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$上,则$\frac{1}{b^2}=1$,即b=1.
又椭圆C的离心率为$\frac{\sqrt{2}}{2}$,则$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,
由a2=b2+c2,得$a=\sqrt{2}$.
∴椭圆C的方程为$\frac{x^2}{2}+{y^2}=1$…(5分)
(Ⅱ)证明:由已知得F(1,0),直线MN的斜率存在.
设直线MN的方程为y=k(x-1),M(x1,y1),N(x2,y2),则P(2,k).
由$\overrightarrow{PM}=λ\overrightarrow{MF}$,$\overrightarrow{PN}=μ\overrightarrow{NF}$,得$λ=\frac{{2-{x_1}}}{{{x_1}-1}},μ=\frac{{2-{x_2}}}{{{x_2}-1}}$,
∴$λ+μ=\frac{{2-{x_1}}}{{{x_1}-1}}+\frac{{2-{x_2}}}{{{x_2}-1}}=\frac{{3({x_1}+{x_2})-2{x_1}{x_2}-4}}{{{x_1}{x_2}-({x_1}+{x_2})+1}}$,.
联立$\left\{{\begin{array}{l}{y=k(x-1)}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$得(1+2k2)x2-4k2x+2k2-2=0.
∴${x_1}+{x_2}=\frac{{4{k^2}}}{{1+2{k^2}}}$,${x_1}{x_2}=\frac{{2{k^2}-2}}{{1+2{k^2}}}$.
∴$3({x_1}+{x_2})-2{x_1}{x_2}-4=3×\frac{{4{k^2}}}{{1+2{k^2}}}-2×\frac{{2{k^2}-2}}{{1+2{k^2}}}-4$=$\frac{{12{k^2}-4{k^2}+4-4-8{k^2}}}{{1+2{k^2}}}$=0,
∴λ+μ=0为定值…(14分)
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,解题时要认真审题,注意函数与方程思想的合理运用,属于中档题.


科目:高中数学 来源: 题型:填空题
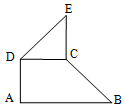 如图,直角梯形ABCD中,AB∥CD,AB⊥AD,AB=2CD=2AD=2.在等腰直角三角形CDE中,∠C=90°,点M,N分别为线段BC,CE上的动点,若$\overrightarrow{AM}•\overrightarrow{AN}=\frac{5}{2}$,
如图,直角梯形ABCD中,AB∥CD,AB⊥AD,AB=2CD=2AD=2.在等腰直角三角形CDE中,∠C=90°,点M,N分别为线段BC,CE上的动点,若$\overrightarrow{AM}•\overrightarrow{AN}=\frac{5}{2}$,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3,-2} | B. | {2,3} | C. | (-3,-2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{3}x$ | B. | $y=-\sqrt{3}x$ | C. | y=2x | D. | y=-2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com