
| ʹ������x | 2 | 3 | 4 | 5 | 6 |
| �ܷ���y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
���� ��1�������ݴ��빫ʽ��������С���˷���ع鷽�̵�ϵ�����ɵûع�ֱ�߷��̣�
��2����x=10����ع鷽�̵�yֵ����ΪԤ��������
��� �⣺��1��$\overline{x}$=4��$\overline{y}$=5��$\sum_{i=1}^{5}$xi2=90��$\sum_{i=1}^{5}$xiyi=112.3��
��$\stackrel{��}{b}$=$\frac{112.3-5��4��5}{90-5��{4}^{2}}$=1.23��$\stackrel{��}{a}$��a=5-1.23��4=0.08��
�����Իع�ֱ�߷�����$\stackrel{��}{y}$=1.23x+0.08��
��2����x=10���꣩ʱ��$\stackrel{��}{y}$=1.23��10+0.08=12.38 ����Ԫ����
������ʹ��10��ʱ��֧���ܷ�����12.38��Ԫ��
���� ���⿼�������Իع�ֱ�߷��̵������ûع鷽�̹���Ԥ������������������Ĺؼ������ù�ʽ��ع鷽�̵�ϵ��������Ҫϸ�ģ�


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | �ཻ | C�� | ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 14 | C�� | 20 | D�� | 35 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
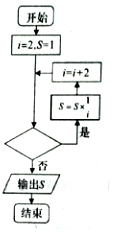 ��ͼ���������Ǽ���������ֵ�ij����ͼ�������жϿ��ڲ������루������
��ͼ���������Ǽ���������ֵ�ij����ͼ�������жϿ��ڲ������루������| A�� | i��2019�� | B�� | i��2019�� | C�� | i��2017�� | D�� | i��2018�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com