
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 相离 |
分析 根据直线与圆相交的弦长公式,求出a的值,结合两圆的位置关系进行判断即可.
解答 解:圆的标准方程为M:x2+(y-a)2=a2 (a>0),
则圆心为(0,a),半径R=a,
圆心到直线x+y=0的距离d=$\frac{a}{\sqrt{2}}$,
∵圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2,
∴2$\sqrt{{a}^{2}-\frac{{a}^{2}}{2}}$=2,
∴a=$\sqrt{2}$,
则圆心为M(0,$\sqrt{2}$),半径R=$\sqrt{2}$,
圆N:(x-1)2+(y-1)2=1的圆心为N(1,1),半径r=1,
则MN=$\sqrt{1+(\sqrt{2}-1)^{2}}$,
∵R+r=$\sqrt{2}$+1,R-r=$\sqrt{2}$-1,
∴R-r<$\sqrt{1+(\sqrt{2}-1)^{2}}$<R+r,
即两个圆相交.
故选:B.
点评 本题主要考查直线和圆相交的应用,以及两圆位置关系的判断,根据相交弦长公式求出a的值是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | {-3,-2} | B. | {2,3} | C. | (-3,-2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 仅有极小值的奇函数 | B. | 仅有极小值的偶函数 | ||
| C. | 仅有极大值的偶函数 | D. | 既有极小值也有极大值的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,4) | B. | ($\frac{2}{3}$,+∞) | C. | (2,+∞) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
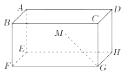 如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.
如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com