Question

9．如图，在四边形ABEF中，AF⊥FB，O为AB的中点，矩形ABCD所在的平面垂直于平面ABEF．
（1）求证：AF⊥平面CBF；
（2）设FC的中点为M，求证：OM∥平面DAF．

Answer 1

分析 （1）欲证AF⊥平面CBF，根据直线与平面垂直的判定定理可知只需证AF与平面CBF内两相交直线垂直，而AF⊥CB，AF⊥BF，BF∩BC=B，满足定理条件；
（2）欲证OM∥平面DAF，根据直线与平面平行的判定定理可知只需证OM/与平面DAF内一直线平行，设DF的中点为N，OM∥AN又AN?平面DAF，OM?平面DAF，满足定理条件．

解答 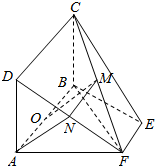（1）证明：∵平面ABCD⊥平面ABEF，CB⊥AB，平面ABCD∩平面ABEF=AB，
∴CB⊥平面ABEF，
∵AF?平面ABEF，
∴AF⊥CB，
又AF⊥BF，且BF∩BC=B，BF、BC?平面CB，
∴AF⊥平面CBF．
（2）证明：设DF的中点为N，则MN$\stackrel{∥}{=}$$\frac{1}{2}$CD，又AO$\stackrel{∥}{=}$$\frac{1}{2}$CD，则MN$\stackrel{∥}{=}$AO，
∴MNAO为平行四边形，
∴OM∥AN，
又AN?平面DAF，OM?平面DAF，
∴OM∥平面DAF．

点评 本题主要考查了直线与平面垂直的判定，以及直线与平面平行的判定，考查空间想象能力、运算能力和推理论证能力，属于中档题．