
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
, ![]()
![]() .
.
(1)证明: ![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
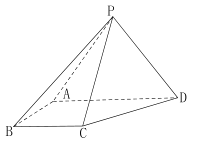
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,由正三角形性质得
,由正三角形性质得![]() ,由矩形的性质得
,由矩形的性质得![]() ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得![]() 平面
平面![]() ,从而可得结论;(2)
,从而可得结论;(2)![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,利用空间向量夹角的余弦公式可得结果.
的法向量,利用空间向量夹角的余弦公式可得结果.
试题解析:(1)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() 为等边三角形,
为等边三角形, ![]() .底面
.底面![]() 中,可得四边形
中,可得四边形![]() 为矩形,
为矩形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .又
.又![]() ,所以
,所以![]() .
.
(2)由面![]() 面
面![]() 知,
知, ![]() 平面
平面![]() ,
, ![]() 两两垂直,直线
两两垂直,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,即
,即![]() ,由
,由![]() ,知
,知![]() ,得
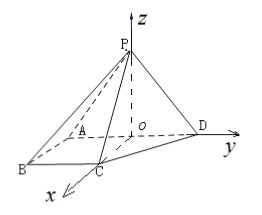
,得![]() .分别以
.分别以![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,则
,则![]()
![]()
![]() ,
, ![]()
![]() , 设平面
, 设平面![]() 的法向量为
的法向量为![]() .
. ,则
,则![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
, 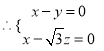 ,则
,则![]() ,
, 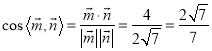 ,
,![]() 由图可知二面角
由图可知二面角![]() 的余弦值
的余弦值![]() .
.
【方法点晴】本题主要考查线面垂直的判定定理以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】1994年到2016年所有关于某项研究成果的540篇论文分布如下图所示.
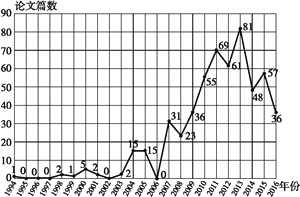
(1)从这540篇论文中随机抽取一篇来研究,那么抽到2016年发表论文的概率是多少?
(2)如果每年发表该领域有国际影响力的论文超过50篇,我们称这一年是该领域的论文“丰年”.若从1994年到2016年中随机抽取连续的两年来研究,那么连续的两年中至少有一年是“丰年”的概率是多少?
(3)由图判断,从哪年开始连续三年论文数量方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|(x﹣3)(x﹣3a﹣5)<0},函数y=lg(﹣x2+5x+14)的定义域为集合B.
(1)若a=4,求集合A∩B;
(2)若“x∈A”是“x∈B”的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() .
.
(1)求圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() ,求直线
,求直线![]() 被圆
被圆![]() 所截得弦长的最大值;
所截得弦长的最大值;
(3)若直线![]() 是圆心
是圆心![]() 下方的切线,当
下方的切线,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有同一型号的电脑96台,为了了解这种电脑每开机一次所产生的辐射情况,从中抽取10台在同一条件下做开机实验,测量开机一次所产生的辐射,得到如下数据:
13.7 12.9 14.4 13.8 13.3
12.7 13.5 13.6 13.1 13.4
(1)写出采用简单随机抽样抽取上述样本的过程;
(2)根据样本,请估计总体平均数与总体标准差的情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在两个正实数m、n,使得等式a(lnn﹣lnm)(4em﹣2n)=3m成立(其中e为自然对数的底数),则实数a的取值范围是( )
A.(﹣∞,0)
B.(0, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞,0)∪[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列4个命题: ①“若a、G、b成等比数列,则G2=ab”的逆命题;
②“如果x2+x﹣6≥0,则x>2”的否命题;
③在△ABC中,“若A>B”则“sinA>sinB”的逆否命题;
④当0≤α≤π时,若8x2﹣(8sinα)x+cos2α≥0对x∈R恒成立,则α的取值范围是0≤α≤ ![]() .
.
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称 | 雅雨 | 雅雨 | 雅女 | 雅竹 | 雅茶 |
月销售额x(万元) | 3 | 5 | 6 | 7 | 9 |
月利润y(万元) | 2 | 3 | 3 | 4 | 5 |
在统计中发现月销售额x和月利润额y具有线性相关关系.
(Ⅰ)根据如下的参考公式与参考数据,求月利润y与月销售额x之间的线性回归方程;
(Ⅱ)若该总公司还有一个分公司“雅果”月销售额为10万元,试求估计它的月利润额是多少?(参考公式: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,其中:
,其中: ![]() =112,
=112, ![]() =200).
=200).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且(a﹣c)(sinA+sinC)=(a﹣b)sinB.
(1)求角C的大小;
(2)若c= ![]() ≤a,求2a﹣b的取值范围.
≤a,求2a﹣b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com