
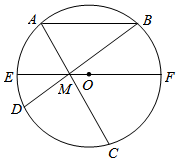
 如图,EF是圆O的直径,AB∥EF,点M在EF上,AM、BM分别交圆O于点C、D.设圆O的半径是r,OM=m.
如图,EF是圆O的直径,AB∥EF,点M在EF上,AM、BM分别交圆O于点C、D.设圆O的半径是r,OM=m.分析 (Ⅰ)作AA′⊥EF交EF于点A′,作BB′⊥EF交EF于点B′.求出A′M和 B′M,可得A′M2+B′M2,从而求得AM2+BM2 的值.
(Ⅱ)因为EM=r-m,FM=r+m,计算AM•CM=r2-m2,代入要求的式子.
解答 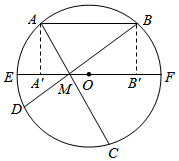 解:(Ⅰ)作AA′⊥EF交EF于点A′,作BB′⊥EF交EF于点B′.
解:(Ⅰ)作AA′⊥EF交EF于点A′,作BB′⊥EF交EF于点B′.
因为A′M=0A′-OM,B′M=OB′+OM=OA′+OM,
所以A′M2+B′M2=2OA′2+2OM2.
从而AM2+BM2=AA′2+A′M2+BB′2+B′M2=2(AA′2+OA′2+OM2),
∴AM2+BM2=2(r2+m2).
(Ⅱ)因为EM=r-m,FM=r+m,
所以AM•CM=BM•DM=EM•FM=r2-m2.
因为$\frac{AM}{CM}$+$\frac{BM}{DM}$=$\frac{{AM}^{2}}{AM•CM}$+$\frac{{BM}^{2}}{BM•DM}$=$\frac{{AM}^{2}{+BM}^{2}}{EM•FM}$,
∴$\frac{AM}{CM}$+$\frac{BM}{DM}$=$\frac{2{(r}^{2}{+m}^{2})}{{r}^{2}{-m}^{2}}$.
又因为r=3m,∴$\frac{AM}{CM}$+$\frac{BM}{DM}$=$\frac{5}{2}$.
点评 本题主要考查与圆有关的比例线段,相交弦定理,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\root{3}{a}$•$\sqrt{-a}$=-a${\;}^{\frac{5}{6}}$ | B. | x${\;}^{\frac{2}{4}}$=$\sqrt{x}$ | C. | ($\root{3}{{b}^{\frac{3}{2}}}$)${\;}^{\frac{3}{2}}$=b3 | D. | (a-b)${\;}^{-\frac{5}{2}}$=$\sqrt{(a-b)^{-5}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,3) | B. | (3,+∞) | C. | ($\frac{1}{2}$,5) | D. | (5,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com