
【题目】如图4,四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,交
,交![]() 于点
于点![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)由![]() 平面
平面![]() ,得到
,得到![]() ,再由四边形
,再由四边形![]() 为正方形得到
为正方形得到![]() ,从而证明
,从而证明![]() 平面
平面![]() ,从而得到
,从而得到![]() ,再结合
,再结合![]() ,即
,即![]() 以及直线与平面垂直的判定定理证明
以及直线与平面垂直的判定定理证明![]() 平面
平面![]() ;(2)先证明
;(2)先证明![]() 、
、![]() 、
、![]() 三条直线两两垂直,然后以点
三条直线两两垂直,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,利用空间向量法求出二面角
轴建立空间直角坐标系,利用空间向量法求出二面角![]() 的余弦值.
的余弦值.
试题解析:(1)![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ;
;
(2)设![]() ,则
,则![]() 中,
中,![]() ,又
,又![]() ,
,
![]() ,
,![]() ,由(1)知
,由(1)知![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() ,同理
,同理![]() ,
,
如图所示,以![]() 为原点,建立空间直角坐标系,则
为原点,建立空间直角坐标系,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
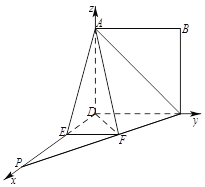
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则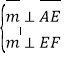 ,又
,又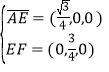 ,
,
所以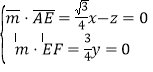 ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
由(1)知平面![]() 的一个法向量
的一个法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,可知
,可知![]() 为锐角,
为锐角,
![]()
![]() ,即所求.
,即所求.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系![]() 的坐标平面
的坐标平面![]() 内,若函数
内,若函数 的图象与
的图象与![]() 轴围成一个封闭区域
轴围成一个封闭区域![]() ,将区域
,将区域![]() 沿
沿![]() 轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域![]() 面积相等,则此圆柱的体积为__________.
面积相等,则此圆柱的体积为__________.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量 ![]() =(2sinA,cos(A﹣B)),
=(2sinA,cos(A﹣B)), ![]() =(sinB,﹣1),且
=(sinB,﹣1),且 ![]()
![]() =
= ![]() .
.
(Ⅰ)求角C的大小;
(Ⅱ)若 ![]() ,求b﹣a的取值范围.
,求b﹣a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校对高二600名学生进行了一次知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(1)填写频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
分组 | 频数 | 频率 |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | |
[80,90) | ||
[90,100] | 14 | 0.28 |
合计 | 1.00 |
如果用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,再从6人中选2人,求2人分数都在[80,90)的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱![]() 容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面
容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面![]() 水平放置,如图所示,点
水平放置,如图所示,点![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在棱
分别在棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 上,水面恰好过点
上,水面恰好过点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() .
.

(1)证明: ![]() ;
;
(2)若底面![]() 水平放置时,求水面的高.
水平放置时,求水面的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式|x+1|+|x﹣1|<4的解集为M.
(1)设Z是整数集,求Z∩M;
(2)当a,b∈M时,证明:2|a+b|<|4+ab|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=3sinx+2cosx+1.若实数a,b,c使得af(x)+bf(x﹣c)=1对任意实数x恒成立,则 ![]() 的值为( )
的值为( )
A.﹣1
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com