
【题目】已知圆C的圆心为原点,且与直线 ![]() 相切.
相切.
(1)求圆C的方程;
(2)点![]() 在直线
在直线![]() 上,过
上,过![]() 点引圆C的两条切线
点引圆C的两条切线![]() ,
, ![]() ,切点为
,切点为![]() ,
, ![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
【答案】解:(1)依题意得:圆![]() 的半径
的半径![]() ,所以圆
,所以圆![]() 的方程为
的方程为![]() 。(4分)
。(4分)
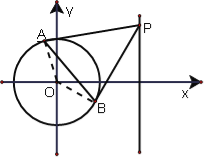
(2)![]() 是圆
是圆![]() 的两条切线,
的两条切线, ![]() 。
。![]() 在以
在以![]() 为直径的圆上。
为直径的圆上。
设点![]() 的坐标为
的坐标为![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为![]() 。
。
![]() 以
以![]() 为直径的圆方程为
为直径的圆方程为![]() (8分)
(8分)
化简得: ![]()
![]() 为两圆的公共弦,
为两圆的公共弦,
![]() 直线
直线![]() 的方程为
的方程为![]()
所以直线![]() 恒过定点
恒过定点![]() 。(12分)
。(12分)
【解析】试题分析:(1)由圆C与直线相切,得到圆心到直线的距离d=r,故利用点到直线的距离公式求出d的值,即为圆C的半径,又圆心为原点,写出圆C的方程即可;
(2)由PA,PB为圆O的两条切线,根据切线的性质得到OA与AP垂直,OB与PB垂直,根据90°圆周角所对的弦为直径可得A,B在以OP为直径的圆上,设出P的坐标为(8,b),由P和O的坐标,利用线段中点坐标公式求出OP中点坐标,即为以OP为直径的圆的圆心坐标,利用两点间的距离公式求出OP的长,即为半径,写出以OP为直径的圆方程,整理后,由AB为两圆的公共弦,两圆方程相减消去平方项,得到弦AB所在直线的方程,可得出此直线方程过(2,0),得证.
解:(1)依题意得:圆心(0,0)到直线![]() 的距离d=r,
的距离d=r,
∴d=![]() ,
,
所以圆C的方程为x2+y2=16①;
(2)连接OA,OB,
∵PA,PB是圆C的两条切线,
∴OA⊥AP,OB⊥BP,
∴A,B在以OP为直径的圆上,
设点P的坐标为(8,b),b∈R,
则线段OP的中点坐标为![]() ,
,
∴以OP为直径的圆方程为![]() ,
,
化简得:x2+y2﹣8x﹣by=0②,b∈R,
∵AB为两圆的公共弦,
∴①﹣②得:直线AB的方程为8x+by=16,b∈R,即8(x﹣2)+by=0,
则直线AB恒过定点(2,0).


科目:高中数学 来源: 题型:
【题目】甲乙两支排球队进行比赛,先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是 ![]() ,其余每局比赛甲队获胜的概率都是
,其余每局比赛甲队获胜的概率都是 ![]() .设各局比赛结果相互独立.
.设各局比赛结果相互独立.
(1)分别求甲队3:0,3:1,3:2胜利的概率;
(2)若比赛结果3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分,求乙队得分X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,F1 , F2分别为椭圆 ![]() +
+ ![]() =1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C. 
(1)若点C的坐标为( ![]() ,
, ![]() ),且BF2=
),且BF2= ![]() ,求椭圆的方程;
,求椭圆的方程;
(2)若F1C⊥AB,求椭圆离心率e的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围是( )
A.![]()
B.k<0或![]()
C.![]()
D.![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,四棱锥P -ABCD的底面是矩形,侧面PAD是正三角形,
且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(1)求证:PB//平面EAC;
(2)求证:AE⊥平面PCD;
(3)当![]() 为何值时,PB⊥AC ?
为何值时,PB⊥AC ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com