
已知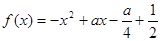 ,
,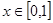 ,
,
(1)求 的最大值
的最大值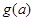 ;
;
(2)求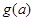 的最小值。
的最小值。
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录。为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足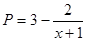 (其中
(其中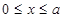 ,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为
,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为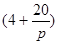 万元/万件.
万元/万件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润是大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一块边长为4米的正方形钢板,现对其进行切割,焊接成一个长方体无盖容器(切、焊损耗忽略不计),有人用数学知识作了如下设计:在钢板的四个角处各切去一个小正方形,剩余部分围成长方体。
(Ⅰ)求这种切割、焊接而成的长方体的最大容积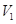 .
.
(Ⅱ)请问:能重新设计,使所得长方体的容器的容积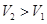 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业生产某种商品 吨,此时所需生产费用为(
吨,此时所需生产费用为(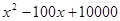 )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为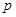 万元,这里
万元,这里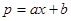 (
(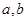 为常数,
为常数,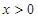 )
)
(1)为了使这种商品的生产费用平均每吨最低,那么这种商品的产量应为多少吨?
(2)如果生产出来的商品能全部卖完,当产量是120吨时企业利润最大,此时出售价格是每吨160万元,求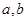 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)已知函数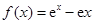 .
.
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)求证: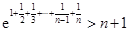
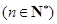 ;
;
(Ⅲ)对于函数 与
与 定义域上的任意实数
定义域上的任意实数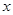 ,若存在常数
,若存在常数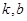 ,使得
,使得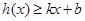 和
和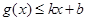 都成立,则称直线
都成立,则称直线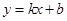 为函数
为函数 与
与 的“分界线”.设函数
的“分界线”.设函数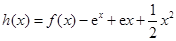 ,
,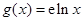 ,
, 与
与 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出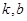 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数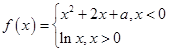 ,其中
,其中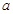 是实数,设
是实数,设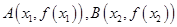 为该函数的图象上的两点,且
为该函数的图象上的两点,且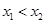 .
.
⑴指出函数 的单调区间;
的单调区间;
⑵若函数 的图象在点
的图象在点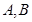 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求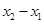 的最小值;
的最小值;
⑶若函数 的图象在点
的图象在点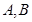 处的切线重合,求
处的切线重合,求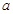 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
运货卡车以每小时 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米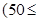
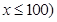 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用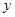 关于
关于 的表达式;
的表达式;
(2)当 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com