
分析 由$\overline{OC}$=-$\frac{1}{6}$(4$\overline{OA}$+5$\overrightarrow{OB}$).两边平方,由外接圆的性质,即可求得cos∠AOB=-$\frac{1}{8}$,且∠ACB=$\frac{1}{2}$∠AOB,根据半角公式即可求得cosC.
解答 解:由O是△ABC外接圆的圆心,则丨$\overline{OA}$丨=丨$\overrightarrow{OB}$丨=丨$\overline{OC}$丨=R,由4$\overline{OA}$+5$\overrightarrow{OB}$+6$\overline{OC}$=$\overrightarrow{0}$,
且$\overline{OC}$=-$\frac{1}{6}$(4$\overline{OA}$+5$\overrightarrow{OB}$).
平方可得 R2=$\frac{1}{36}$(16R2+40R2cos∠AO,B+25R2),解得:cos∠AOB=-$\frac{1}{8}$,
由∠ACB=$\frac{1}{2}$∠AOB,
则cos∠ACB=cos$\frac{1}{2}$∠AOB=$\sqrt{\frac{1+cos∠AOB}{2}}$=$\frac{\sqrt{7}}{4}$,
则cosC=$\frac{\sqrt{7}}{4}$,
故答案为:$\frac{\sqrt{7}}{4}$.
点评 本题考查向量的运算和三角形外心的性质和应用,半角公式,解题时要认真审题,仔细解答,注意向量运算法则的灵活运用,属于中档题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
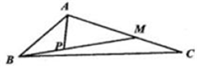 如图,已知△ABC中,点M在线段AC上,点P在线段BM上,且满足$\frac{AM}{MC}$=$\frac{MP}{PB}$=2,若|${\overrightarrow{AB}}$|=2,|${\overrightarrow{AC}}$|=3,∠BAC=120°,则$\overrightarrow{AP}$•$\overrightarrow{BC}$的值为-2.
如图,已知△ABC中,点M在线段AC上,点P在线段BM上,且满足$\frac{AM}{MC}$=$\frac{MP}{PB}$=2,若|${\overrightarrow{AB}}$|=2,|${\overrightarrow{AC}}$|=3,∠BAC=120°,则$\overrightarrow{AP}$•$\overrightarrow{BC}$的值为-2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x3 | B. | 1+x | C. | cosx | D. | xex |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com