
设 圆
圆 与
与 轴正半轴的交点为
轴正半轴的交点为 ,与曲线
,与曲线 的交点为
的交点为 ,直线
,直线 与
与 轴的交点为
轴的交点为 .
.
(1)用 表示
表示 和
和
(2)若数列 满足
满足
(1)求常数 的值,使得数列
的值,使得数列 成等比数列;
成等比数列;
(2)比较 与
与 的大小.
的大小.
(1) ,
, ;(2)当
;(2)当 时,数列
时,数列 成公比为4的等比数列;当
成公比为4的等比数列;当 时,数列
时,数列 成公比为2的等比数列.
成公比为2的等比数列. .
.
【解析】
试题分析:本题主要考查曲线与圆相交问题、直线的方程、等比数列的证明、利用导数判断函数的单调性等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,点N代入到曲线 和圆中,联立得到
和圆中,联立得到 ,由于直线MN过M、A点,从而得到直线MN的方程,N点也在MN上,代入MN方程中,经整理得到
,由于直线MN过M、A点,从而得到直线MN的方程,N点也在MN上,代入MN方程中,经整理得到 的表达式;第二问,(ⅰ)利用等比数列的定义知
的表达式;第二问,(ⅰ)利用等比数列的定义知 为等比数列,利用等比数列的通项公式,经过化简得
为等比数列,利用等比数列的通项公式,经过化简得 ,利用
,利用 的通项公式和
的通项公式和 为等比数列列出2个关系式,利用2个式子是q倍的关系,解出p和q的值;(ⅱ)利用
为等比数列列出2个关系式,利用2个式子是q倍的关系,解出p和q的值;(ⅱ)利用 可以猜想
可以猜想 ,即需要证
,即需要证 ,构造函数
,构造函数 ,利用导数判断函数
,利用导数判断函数 的单调性,从而确定
的单调性,从而确定 ,即
,即 ,所以
,所以 .
.
试题解析:(1) 与圆
与圆 交于点
交于点 ,则
,则 ,即
,即 .由题可知,点
.由题可知,点 的坐标为
的坐标为 ,从而直线
,从而直线 的方程为
的方程为 ,由点
,由点 在直线
在直线 上得
上得 ,将
,将 ,
, 代入,
代入,
得 ,
,
 即
即 4分
4分
(2)由 知,
知, 为等比数列,由
为等比数列,由 ,
, 知,公比为4,故
知,公比为4,故 ,所以
,所以 5分
5分
(1)


令 得
得

由等式
对于任意 成立,得
成立,得
 解得
解得 或
或 8分
8分
故当 时,数列
时,数列 成公比为4的等比数列;
成公比为4的等比数列;
当 时,数列
时,数列 成公比为2的等比数列. 9分
成公比为2的等比数列. 9分
(2)由(1)知 ,当
,当 时,
时,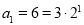 ;当
;当 时,
时, 事实上,令
事实上,令 ,则
,则 故
故
 是增函数,所以
是增函数,所以 ,即
,即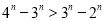
即 . 14分
. 14分
考点:曲线与圆相交问题、直线的方程、等比数列的证明、利用导数判断函数的单调性.


科目:高中数学 来源:2013-2014学年福建省高三高考压轴理科数学试卷(解析版) 题型:选择题
下列命题正确的是( )
A.存在x0∈R,使得 的否定是:不存在x0∈R,使得
的否定是:不存在x0∈R,使得 ;
;
B.存在x0∈R,使得 的否定是:任意x∈R,均有
的否定是:任意x∈R,均有
C.若x=3,则x2-2x-3=0的否命题是:若x≠3,则x2-2x-3≠0.
D.若 为假命题,则命题p与q必一真一假
为假命题,则命题p与q必一真一假
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:选择题
已知直线a,b异面, ,给出以下命题:①一定存在平行于a的平面
使 ;②一定存在平行于a的平面
;②一定存在平行于a的平面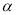 使
使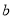 ∥
∥ ;③一定存在平行于a的平面
;③一定存在平行于a的平面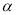 使
使 ;④一定存在无数个平行于a的平面
;④一定存在无数个平行于a的平面 与b交于一定点.则其中论断正确的是( )
与b交于一定点.则其中论断正确的是( )
A.①④ B.②③ C.①②③ D.②③④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟理科数学试卷(解析版) 题型:填空题
已知集合 ,若对于任意实数对
,若对于任意实数对 ,存在
,存在 ,使得
,使得 成立,则称集合
成立,则称集合 为“正交点集”,给出下列集合:
为“正交点集”,给出下列集合:
① ;②
;② ;③
;③ ;
;
④ ;⑤
;⑤ .
.
则满足条件的“正交集合”有:_________________________(写出所有满足条件的集合的序号)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟理科数学试卷(解析版) 题型:选择题
已知曲线 :
: 和
和 :
: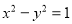 ,且曲线
,且曲线 的焦点分别为
的焦点分别为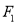 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试理科数学试卷(解析版) 题型:选择题
已知圆 和圆
和圆 ,动圆M与圆
,动圆M与圆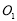 ,圆
,圆 都相切,动圆的圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为
都相切,动圆的圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为 ,
, (
(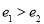 ),则
),则 的最小值是( )
的最小值是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com