
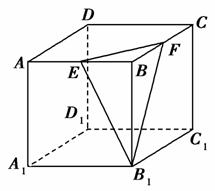
在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、BC的中点,则点C1到平面B1EF的距离等于( )
A.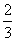 B.
B.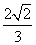
C.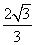 D.
D.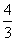
科目:高中数学 来源: 题型:
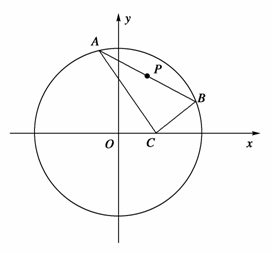
已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足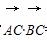 =0,设P为弦AB的中点.
=0,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线x=-1的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
在三棱柱ABC-A′B′C′中,已知AA′⊥平面ABC,AA′=2,BC=2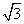 ,∠BAC=
,∠BAC=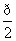 ,且此三棱柱的各个顶点都在一个球面上,则球的体积为________.
,且此三棱柱的各个顶点都在一个球面上,则球的体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC= AD=1.
AD=1.
(1)求证:平面PAC⊥平面PCD;
(2)在棱PD上是否存在一点E,使CE∥平面PAB?若存在,请确定E点的位置;若不存在,请说明理由.
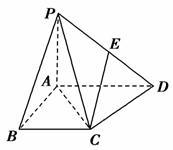
查看答案和解析>>
科目:高中数学 来源: 题型:
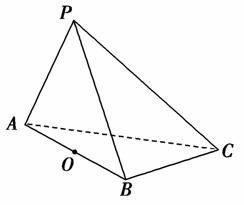
在三棱锥P-ABC中,△PAC和△PBC是边长为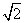 的等边三角形,AB=2,O是AB的中点.
的等边三角形,AB=2,O是AB的中点.
(1)在棱PA上求一点M,使得OM∥平面PBC;
(2)求证:平面PAB⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
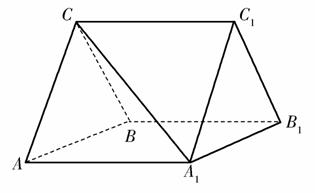
(1)证明:AB⊥A1C;
(2)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的,其中AB=4,BC=2,CC1=3,BE=1.
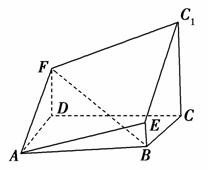
(1)求BF的长;
(2)求点C到平面AEC1F的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,正方体ABCD-A1B1C1D1的棱长为2.动点E、F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P-EFQ的体积( )
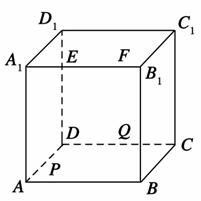
A.与x、y都有关
B.与x、y都无关
C.与x有关,与y无关
D.与y有关,与x无关
查看答案和解析>>
科目:高中数学 来源: 题型:
已知l是直线,α、β是两个不同平面,下列命题中的真命题是( )
A.若l∥α,l∥β,则α∥β
B.若α⊥β,l∥α,则l⊥β
C.若l⊥α,l∥β,则α⊥β
D.若l∥α,α∥β,则l∥β
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com