
在三棱锥P-ABC中,△PAC和△PBC是边长为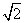 的等边三角形,AB=2,O是AB的中点.
的等边三角形,AB=2,O是AB的中点.
(1)在棱PA上求一点M,使得OM∥平面PBC;
(2)求证:平面PAB⊥平面ABC.
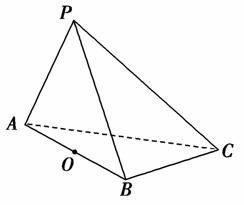
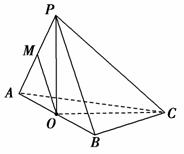
解法一:(1)当M为棱PA的中点时,OM∥平面PBC.
证明如下:
∵M,O分别为PA,AB的中点,
∴OM∥PB.
又PB⊂平面PBC,OM⊄平面PBC,
∴OM∥平面PBC.
(2)连接OC,OP.
∵AC=CB=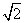 ,O为AB的中点,AB=2,
,O为AB的中点,AB=2,
∴OC⊥AB,OC=1.
同理,PO⊥AB,PO=1.
又PC=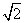 ,∴PC2=OC2+PO2=2,
,∴PC2=OC2+PO2=2,
∴∠POC=90°,∴PO⊥OC.
∵AB∩OC=O,
∴PO⊥平面ABC.
∵PO⊂平面PAB,
∴平面PAB⊥平面ABC.
解法二:设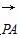 =a,
=a, =b,
=b,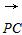 =c,则由条件知|a|=|b|=|c|=
=c,则由条件知|a|=|b|=|c|=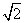 ,a·c=b·c=1,
,a·c=b·c=1,
在△PAB中,PA=PB=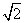 ,AB=2,∴PA⊥PB,∴a·b=0.
,AB=2,∴PA⊥PB,∴a·b=0.
(1)设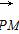 =λa,则
=λa,则 =
=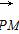 -
-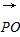 =λa-
=λa- (a+b)=(λ-
(a+b)=(λ- )a-
)a- b,
b,
∵OM∥平面PBC,
∴存在实数s,k,使 =sb+kc,
=sb+kc,
∴sb+kc=(λ- )a-
)a- b,
b,
由平面向量基本定理知,λ= ,s=-
,s=- ,k=0,
,k=0,
∴M为PA的中点.
(2) 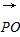 =
= (a+b),
(a+b),
∵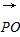 ·
·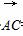 =
= (a+b)·(c-a)
(a+b)·(c-a)
= (a·c+b·c-|a|2-a·b)=0,
(a·c+b·c-|a|2-a·b)=0,
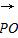 ·
·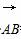 =
= (a+b)·(b-a)=
(a+b)·(b-a)= (|b|2-|a|2)=0,
(|b|2-|a|2)=0,
∴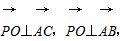
∴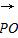 是平面ABC的法向量,
是平面ABC的法向量,
又PO⊂平面PAB,
∴平面PAB⊥平面ABC.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
设平面区域D是由双曲线y2-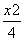 =1的两条渐近线和抛物线y2=-8x的准线所围成的三角形(含边界与内部).若点(x,y)∈D,则x+y的最小值为( )
=1的两条渐近线和抛物线y2=-8x的准线所围成的三角形(含边界与内部).若点(x,y)∈D,则x+y的最小值为( )
A.-1 B.0
C.1 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
在如图所示的几何体中,四边形ABCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.
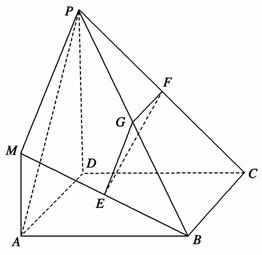
(1)求证:平面EFG⊥平面PDC;
(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
平面α经过三点A(-1,0,1)、B(1,1,2),C(2,-1,0),则下列向量中与平面α的法向量不垂直的是( )
A. 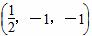 B.(6,-2,-2)
B.(6,-2,-2)
C.(4,2,2) D.(-1,1,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
.如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
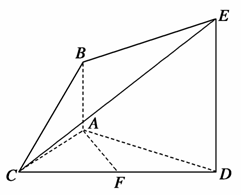
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在斜三棱柱ABC-A1B1C1中,点O、E分别是A1C1、AA1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.

(1)证明:OE∥平面AB1C1;
(2)求异面直线AB1与A1C所成的角;
(3)求A1C1与平面AA1B1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在△ABC中,∠C=90°,∠A=30°,BC=1.在三角形内挖去半圆(圆心O在边AC上,半圆分别与BC、AB相切于点C、M,与AC交于点N),则图中阴影部分绕直线AC旋转一周所得旋转体的体积为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
空间中一条线段AB的三视图中,俯视图是长度为1的线段,侧视图是长度为2的线段,则线段AB的长度的取值范围是( )
A.(0,2] B.[2,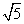 ]
]
C.[2,3] D.[2,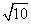 ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com