
【题目】命题p:实数x满足x2﹣4ax+3a2<0(其中a>0),命题q:实数x满足 
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
【答案】
(1)解:∵a=1,p∧q为真,∴p,q都为真.
p:x2﹣4x+3<0,解得1<x<3.
命题q:实数x满足 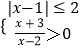 ,化为
,化为 ![]() ,解得2<x≤3.
,解得2<x≤3.
∴ ![]() ,解得2<x<3.
,解得2<x<3.
∴实数x的取值范围是2<x<3
(2)解:命题p:实数x满足x2﹣4ax+3a2<0(其中a>0),解得a<x<3a.
¬p:x≤a或x≥3a.
q:2<x≤3,则¬q:x≤2或x>3.
∵¬p是¬q的充分不必要条件,
∴ ![]() ,解得1<a≤2.
,解得1<a≤2.
∴实数a的取值范围是(1,2]
【解析】(1)由a=1,p∧q为真,可得p,q都为真.分别化简命题p,q即可得出.(2)命题p:实数x满足x2﹣4ax+3a2<0(其中a>0),利用一元二次不等式的解法可得解得a<x<3a.¬p,q:2<x≤3,则¬q:x≤2或x>3.利用¬p是¬q的充分不必要条件,即可得出.
【考点精析】解答此题的关键在于理解复合命题的真假的相关知识,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


科目:高中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且 ![]() ,
, ![]() ,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则
,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则 ![]() 的最小值为 .
的最小值为 . 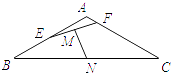
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式f(x)= ![]() ﹣
﹣ ![]() (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一河南旅游团到安徽旅游.看到安徽有很多特色食品,其中水果类较有名气的有:怀远石榴、砀山梨、徽州青枣等19种,点心类较有名气的有:一品玉带糕、徽墨酥、八公山大救驾等38种,小吃类较有名气的有:符离集烧鸡、无为熏鸭、合肥龙虾等57种.该旅游团的游客决定按分层抽样的方法从这些特产中买6种带给亲朋品尝.
(1)求应从水果类、点心类、小吃类中分别买回的种数;
(2)若某游客从买回的6种特产中随机抽取2种送给自己的父母,
①列出所有可能的抽取结果;
②求抽取的2种特产均为小吃的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,现要在一块半径为1m,圆心角为 ![]() 的扇形纸报AOB上剪出一个平行四边形MNPQ,使点P在弧AB上,点Q在OA上,点M、N在OB上,设∠BOP=θ,平行四边形MNPQ的面积为S.
的扇形纸报AOB上剪出一个平行四边形MNPQ,使点P在弧AB上,点Q在OA上,点M、N在OB上,设∠BOP=θ,平行四边形MNPQ的面积为S. 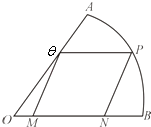
(1)求S关于θ的函数关系式;
(2)求S的最大值及相应的θ角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点. 
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com