Question

11．三棱锥S-ABC中，AB=BC=AC=2，SC=4，SA=SB，SC与平面ABC所成角的余弦值是$\frac{{\sqrt{3}}}{3}$，若S，A，B，C都在同一球面上，则该球的表面积是（　　）

• A． 4π
• B． 8π
• C． 16π
• D． 64π

Answer 1

分析 取AB中点，连结SD，CD，∠SCD就是SC与平面ABC所成角，在△SDC中，由余弦定理得SD、SA、SB，由SA²+AC²=SC²，SB²+BC²=SC²得SC 的中点为三棱锥S-ABC外接球的球心，半径即可

解答 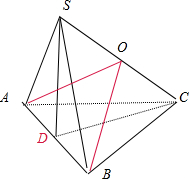解：如图取AB中点，连结SD，CD，
∵AB=BC=AC=2，SA=SB，∴CD⊥AB，SD⊥AB，CD=$\sqrt{3}$，
⇒AB⊥面SDC，∴面SDC⊥面ABC，
∴∠SCD就是SC与平面ABC所成角，
在△SDC中，由余弦定理得SD=$\sqrt{11}$．
从而得到SA=SB=2$\sqrt{3}$，
∴SA²+AC²=SC²，SB²+BC²=SC²，
∴△ACS，△CBS，有公共斜边SC，故SC 的中点为三棱锥S-ABC外接球的球心，半径为2，
该球的表面积s=4πR²=16π，
故选：C．

点评 本题考查了三棱锥的外接球，关键是找到球心，求出半径，属于中档题．