练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．设i为虚数单位，则（x-i）6的展开式中含x4的项为（　　）
    A．-15x4B．15x4C．-20ix4D．20ix4

    分析 在二项式展开式的通项公式中，令x的幂指数等于4，求得r的值，可得展开式中含x4的项．

    解答 解：（x-i）6的展开式的通项公式为Tr+1=${C}_{6}^{r}$•x6-r•（-i）r，令6-r=4，求得r=2，
    故展开式中含x4的项为${C}_{6}^{2}$•（-i）2•x4=-15x4，
    故选：A．

    点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．已知函数f（x）对任意自然数x，y均满足：f（x+y2）=f（x）+2[f（y）]2，且f（1）≠0，则f（2014）=（　　）
    A．1007B．1006C．2014D．2013

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知f （x）=xlnx．
    （I）求f （x） 在[t，t+2]（t是大于0的常数）上的最小值；
    （Ⅱ）证明：?x∈（0，+∞）都有1nx＞$\frac{1}{e^x}$-$\frac{2}{ex}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．?x∈R，ex≥ax+b，则实数a，b的乘积a•b的最大值为（　　）
    A．$\frac{e}{2}$B．2C．1D．$\frac{e}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知函数f（x）=$\left\{\begin{array}{l}{e^x}+{x^2}，x≥0\\{e^{-x}}+{x^2}，x＜0\end{array}$，若f（-a）+f（a）≤2f（1），则a的取值范围是（　　）
    A．（-∞，1]∪[1，+∞）B．[-1，0]C．[0，1]D．[-1，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．某市乘坐出租车的收费办法如表：
    （1）不超过4千米的里程收费12元；
    （2）超过4千米的里程按每千米2元收费（对于其中不足千米的部分，若其小于0.5千米则不收费，若其大于或等于0.5千米则按1千米收费）；
    当车程超过4千米时，另收燃油附加费1元．
    相应系统收费的程序框图如图所示，其中x（单位：千米）为行驶里程，y（单位：元）为所收费用，用[x]表示不大于x的最大整数，则图中①处应填（　　）
    A．y=2[x+$\frac{1}{2}$]+4B．y=2[x+$\frac{1}{2}$]+5C．y=2[x-$\frac{1}{2}$]+4D．y=2[x+$\frac{1}{2}$]+5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

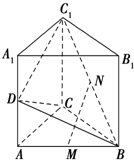    20．如图，已知直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=BC=2，AA1=4，D是棱AA1上的一点，M，N分别为BC1AB，的中点．
    （1）求证：MN∥平面DCC1；
    （2）当D为AA1的中点时，求三棱锥D-ACN的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数f（x）=$\left\{\begin{array}{l}{x-2+\frac{1}{x-2}，x＞2}\\{-\frac{1}{x-2}-1，1＜x＜2}\\{-x+1，x≤1}\end{array}\right.$，g（x）=$\frac{1}{3}$x+m，若函数h（x）=f（x）-g（x）有四个零点，则实数m的取值范围是（1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．定义在[-2，2]上的偶函数f（x）在[-2，0]上是减函数，若f（x+1）＜f（2x），则实数x的取值范围是（　　）
    A．[-1，-$\frac{1}{3}$）B．[-2，$\frac{1}{3}$）C．（-$\frac{1}{3}$，1]D．（1，2]

    查看答案和解析>>

    同步练习册答案