
已知数列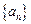 的前
的前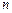 项和为
项和为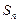 ,
,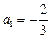 ,满足
,满足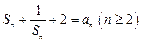
(1)计算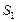 、
、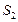 、
、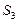 、
、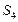 ,并猜想
,并猜想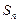 的表达式;
的表达式;
(2)用数学归纳法证明你猜想的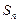 的表达式。(13分)
的表达式。(13分)
 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
有6本不同的书,按照以下要求处理,各有多少种不同的分法?
(1)一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得二本,一人得三本;
(4)平均分给甲、乙、丙三人;
(5)平均分成三堆.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
5个人排成一排,按下列要求各有多少种不同的排法?
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙2人必须相邻;
(3)其中甲、乙2人不能相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲只能站在乙的左侧.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)有4名老师和4名学生站成一排照相。
(I)4名学生必须排在一起,共有多少种不同的排法?
(II)任两名学生都不能相邻,共有多少种不同的排法?
(III)老师和学生相间排列,共有多少种不同的排法?(要求用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com