
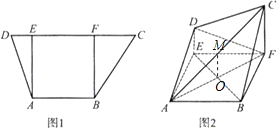
【题目】如图1,在梯形ABCD中,AB//CD,AB=3,CD=6,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=3,将梯形ABCD沿AE,BF同侧折起,使得平面ADE⊥平面ABFE,平面ADE∥平面BCF,得到图2.
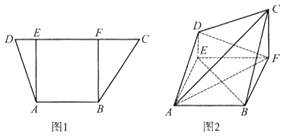
(1)证明:BE//平面ACD;
(2)求三棱锥C﹣AED的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设AF∩BE=O,取AC中点M,连接OM,证明四边形DEOM为平行四边形,从而得到DM//OE,再利用线面平行判定定理证得结论;
(2)由点C到平面ADE的距离等于点F到平面ADE的距离,即可得到![]()
将数据代入即可得答案.
(1)证明:设AF∩BE=O,取AC中点M,连接OM.
∵四边形ABFE为正方形,∴O为AF中点,
∵M为AC中点,∴![]() ,
,![]() .
.
∵平面ADE![]() 平面ABFE,平面ADE
平面ABFE,平面ADE![]() 平面ABFE
平面ABFE![]() AE,DE
AE,DE![]() AE,DE
AE,DE![]() 平面ADE,
平面ADE,
∴DE![]() 平面ABFE;
平面ABFE;
又∵平面ADE//平面BCF,∴平面BCF⊥平面ABFE,同理,CF⊥平面ABFE.
又∵DE=1,FC=2,∴![]() 且
且![]() ,
,
∴![]() ,且OM
,且OM![]() DE,∴四边形DEOM为平行四边形,∴DM//OE.
DE,∴四边形DEOM为平行四边形,∴DM//OE.
∵DM平面ADC,BE平面ADC,∴BE//平面ADC.
(2)∵CF![]() DE,DE
DE,DE![]() 平面ADE,CF
平面ADE,CF![]() 平面ADE,
平面ADE,
∴CF![]() 平面ADE,
平面ADE,
∴点C到平面ADE的距离等于点F到平面ADE的距离.
∴![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为
分别为![]() 的上、下顶点且
的上、下顶点且![]() 为
为![]() 外的动点,且
外的动点,且![]() 到
到![]() 上点的最近距离为1.
上点的最近距离为1.
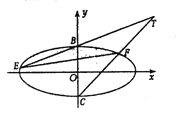
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,设直线
时,设直线![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,求
倍,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,又在直角坐标系
,又在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数).
(t为参数).
(1)求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() 在曲线
在曲线![]() 上,点Q在曲线
上,点Q在曲线![]() 上,若
上,若![]() 的最小值为
的最小值为![]() ,求此时点
,求此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,正确的是( )
旋转过程中的一个图形,下列命题中,正确的是( )

A.动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
B.恒有平面![]() 平面
平面![]()
C.三棱锥![]() 的体积有最大值
的体积有最大值
D.旋转过程中二面角![]() 的平面角始终为
的平面角始终为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() 上一点
上一点![]() 到焦点的距离为3.
到焦点的距离为3.
(1)求曲线C方程;
(2)设P,Q为曲线C上不同于原点O的任意两点,且满足以线段PQ为直径的圆过原点O,试问直线PQ是否恒过定点?若恒过定点,求出定点坐标;若不恒过定点,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com