
【题目】设![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和,且
项和,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若满足不等式![]() 的正整数
的正整数![]() 恰有
恰有![]() 个,求正实数
个,求正实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】若函数f(x)![]() (c≠0),其图象的对称中心为(
(c≠0),其图象的对称中心为(![]() ,
,![]() ),现已知f(x)
),现已知f(x)![]() ,数列{an}的通项公式为an=f(
,数列{an}的通项公式为an=f(![]() )(n∈N+),则此数列前2020项的和为_____.
)(n∈N+),则此数列前2020项的和为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 上各点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上各点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() .
.
(1)求直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AB//CD,AB=3,CD=6,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=3,将梯形ABCD沿AE,BF同侧折起,使得平面ADE⊥平面ABFE,平面ADE∥平面BCF,得到图2.
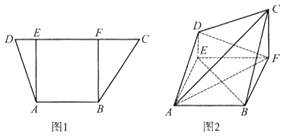
(1)证明:BE//平面ACD;
(2)求三棱锥C﹣AED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,
,![]() ,
,![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若对![]() ,都有
,都有![]() ,求实数a的取值范围;
,求实数a的取值范围;
(3)当![]() 时,将数列
时,将数列![]() 中的部分项按原来的顺序构成数列
中的部分项按原来的顺序构成数列![]() 且
且![]() 证明:存在无数个满足条件的无穷等比数列
证明:存在无数个满足条件的无穷等比数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日全面实施二孩政策以来,为了了解生二孩意愿与年龄段是否有关,某市选取“75后”和“80后”两个年龄段的已婚妇女作为调查对象,进行了问卷调查,共调查了40名“80后”,40名“75后”,其中调查的“80后”有10名不愿意生二孩,其余的全部愿意生二孩;调查的“75后”有5人不愿意生二孩,其余的全部愿意生二孩.
(1)根据以上数据完成下列![]() 列联表;
列联表;
年龄段 | 不愿意 | 愿意 | 合计 |
“80后” | |||
“75后” | |||
合计 |
(2)根据![]() 列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
参考公式: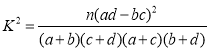 (其中
(其中![]() )
)
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 在圆
在圆![]() 上运动,
上运动,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求证:![]() 为定值及动点
为定值及动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)不在![]() 轴上的
轴上的![]() 点为
点为![]() 上任意一点,
上任意一点,![]() 与
与![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 交
交![]() 于另外一点
于另外一点![]() .求证:直线
.求证:直线![]() 与直线
与直线![]() 的斜率的乘积为定值,并求出该定值.
的斜率的乘积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com