Question

2．已知a∈R，函数f（x）=（x-a）|x-1|．
（Ⅰ）若a=3，求f（x）的单调递增区间；
（Ⅱ）函数f（x）在[a-$\sqrt{2}$+1，b]上的值域为[-1，1]，求a，b需要满足的条件．

Answer 1

分析 （Ⅰ）去绝对值号得到$f（x）=\left\{\begin{array}{l}{{x}^{2}-4x+3}&{x≥1}\\{-{x}^{2}+4x-3}&{x＜1}\end{array}\right.$，然后根据二次函数单调区间的求法，求每段上f（x）的单调递增区间即可；
（Ⅱ）对每段上f（x）进行配方，便可得到f（x）=（x-2）²-1，x≥1，f（x）=-（x-2）²+1，x＜1，从而可画出f（x）的大致图象，根据图象即可得出区间$[a-\sqrt{2}+1，b]$的两端点满足的条件，从而得出a，b满足的条件．

解答 解：（Ⅰ）a=3时，$f（x）=（x-3）|x-1|=\left\{\begin{array}{l}{{x}^{2}-4x+3}&{x≥1}\\{-{x}^{2}+4x-3}&{x＜1}\end{array}\right.$；
①x≥1时，f（x）=x²-4x+3；
∴f（x）在[2，+∞）上单调递增；
②x＜1时，f（x）=-x²+4x-3；
∴f（x）在（-∞，1）上单调递增；
∴f（x）的单调递增区间为（-∞，1），[2，+∞）；
（Ⅱ）$f（x）=\left\{\begin{array}{l}{{x}^{2}-（a+1）x+a}&{x≥1}\\{-{x}^{2}+（a+1）x-a}&{x＜1}\end{array}\right.$；
可以画出f（x）的大致图象为：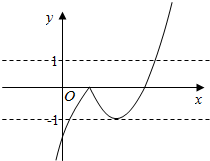

（1）若a＞1；
①$\frac{-（a-1）^{2}}{4}＜-1$，即a＞3；
解x²-（a+1）x+a=-1得，x=$\frac{a+1±\sqrt{{a}^{2}-2a-3}}{2}$；
∴$\frac{a+1+\sqrt{{a}^{2}-2a-3}}{2}=a-\sqrt{2}+1$，∴$a=2\sqrt{2}+1$，满足a＞3；
令x²-4x+3=1得，$x=2±\sqrt{2}$，b=2$+\sqrt{2}$；
②$\frac{-（a-1）^{2}}{4}=-1$，∴a=3；
∴$f（x）=\left\{\begin{array}{l}{{x}^{2}-4x+3}&{x≥1}\\{-{x}^{2}+4x-3}&{x＜1}\end{array}\right.$；
令-x²+4x-3=-1得，$x=2±\sqrt{2}$，令x²-4x+3=1得，$x=2±\sqrt{2}$；
∴$2-\sqrt{2}≤a-\sqrt{2}+1≤2，b=2+\sqrt{2}$；
即$1≤a≤1+\sqrt{2}，b=2+\sqrt{2}$；
③$\frac{-（a-1）^{2}}{4}＞-1$，即1＜a＜3；
解-x²+（a+1）x-a=-1得，$x=\frac{a+1±\sqrt{{a}^{2}-2a+5}}{2}$；
∴$\frac{a+1-\sqrt{{a}^{2}-2a+5}}{2}=a-\sqrt{2}+1$，则a=-1，与1＜a＜3矛盾，即这种情况不存在；
（2）若a=1，$f（x）=\left\{\begin{array}{l}{（x-1）^{2}}&{x≥1}\\{-（x-1）^{2}}&{x＜1}\end{array}\right.$；
则由上面知a=-1，与a=1矛盾，即这种情况不存在；
（3）若a＜1，则：
①$\frac{-（a-1）^{2}}{4}＜-1$时，即a＜-1，由上面求出a=$2\sqrt{2}+1$，不满足a＜-1，这种情况不存在；
②$\frac{-（a-1）^{2}}{4}＞-1$时，即-1＜a＜1，由上面求出a=-1，不符合-1＜a＜1；
综上得$1≤a≤1+\sqrt{2}$，b=$2+\sqrt{2}$，或a=$2\sqrt{2}+1$，$b=2+\sqrt{2}$．

点评 考查含绝对值函数的处理方法：去绝对值号，二次函数及分段函数单调区间的求法，函数值域的概念，根据函数图象解决问题的方法．