
分析 (1)、分A=∅和A≠∅的情况,然后根据条件证明即可.
(2)、理解A=B≠∅表示方程ax2-1=x与方程a(ax2-1)2-1=x有相同的根,从而化简求解.
解答 解:(1)证明:若A=∅,则A⊆B显然成立;
若A≠∅,设t∈A,则f(t)=t,f(f(t))=f(t)=t,
∴t∈B,故A⊆B.
(2)∵A≠∅,∴ax2-1=x有实根,
∴a≥-$\frac{1}{4}$.
∵a(ax2-1)2-1=x,
∴(ax2-x-1)(a2x2+ax-a+1)=0.
∵A=B,
∴a2x2+ax-a+1=0没有实根或实根是方程ax2-x-1=0的根.
若a2x2+ax-a+1=0没有实根,
则a<$\frac{3}{4}$;
若a2x2+ax-a+1=0有实根且实根是方程ax2-x-1=0的根,
则由方程ax2-x-1=0得a2x2=ax+a,
代入a2x2+ax-a+1=0得2ax+1=0.
由此解得x=-$\frac{1}{2a}$,再代入得
$\frac{1}{4a}$+$\frac{1}{2a}$-1=0,
由此a=$\frac{3}{4}$,
故a的取值范围是[-$\frac{1}{4}$,$\frac{3}{4}$].
点评 本题考查对新概念的理解和运用的能力,同时考查了集合间的关系和方程根的相关知识,解题过程中体现了分类讨论的数学思想.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
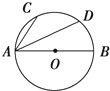 如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )
如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )| A. | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com