
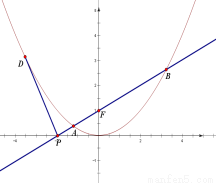
抛物线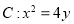 ,直线
,直线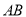 过抛物线
过抛物线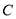 的焦点
的焦点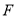 ,交
,交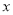 轴于点
轴于点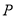 .
.
(1)求证: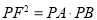 ;
;
(2)过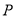 作抛物线
作抛物线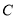 的切线,切点为
的切线,切点为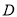 (异于原点),
(异于原点),
(i)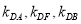 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ii)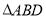 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
(1)即证 (2)能抛物线
(2)能抛物线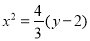
【解析】
试题分析:(1)由于点F的坐标已知,所以可假设直线AB的方程(依题意可得直线AB的斜率存在).写出点P的坐标,联立直线方程与抛物线方程消去y,即可得到一个关于x的一元二次方程,写出韦达定理,再根据欲证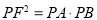 转化为点的坐标关系.
转化为点的坐标关系.
(2)(i)根据提议分别写出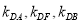 ,结合韦达定理验证
,结合韦达定理验证 是否成立.
是否成立.
(ii)由三角形重心的坐标公式,结合韦达定理,消去参数k即可得到重心的轨迹.
试题解析:(1)因为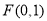 ,所以假设直线AB为
,所以假设直线AB为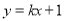 ,
, ,所以点
,所以点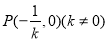 .联立
.联立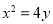 可得,
可得, ,所以
,所以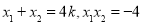 .因为
.因为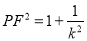 ,
,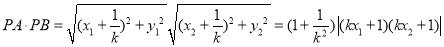
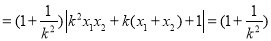 .所以
.所以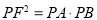 .
.
(2)(i)设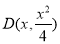 ,
,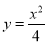 的导数为
的导数为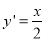 .所以可得
.所以可得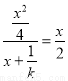 ,即可得
,即可得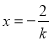 .即得
.即得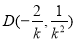 .
.
 .
.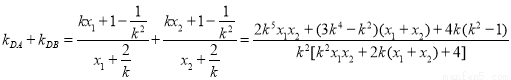
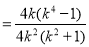
 .所以可得
.所以可得 即
即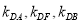 是否恒成等差数列.
是否恒成等差数列.
(ii)因为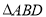 重心的坐标为
重心的坐标为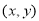 由题意可得
由题意可得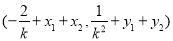 .即
.即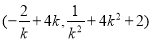 ,
, 消去k可得
消去k可得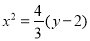 .
.
考点:1.抛物线的性质.2.解方程的思想.3.等差数列的证明.4.三角形的重心的公式.5.运算能力.6.分析问题和解决问题的能力、以及等价转化的数学思想.


科目:高中数学 来源:2013-2014学年湖北省黄冈市高三5月适应性考试理科数学试卷(解析版) 题型:选择题
非零向量 与
与 满足
满足 且
且 ,则⊿ABC为( )
,则⊿ABC为( )
A.三边均不等的三角形 B.直角三角形
C.等边三角形 D.等腰非等边三角形
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省黄冈市高三第二学期三月月考文科数学试卷(解析版) 题型:填空题
设x,y满足 若目标函数z=ax+y(a>0)的最大值为14,则a=
若目标函数z=ax+y(a>0)的最大值为14,则a=
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省黄冈市高三下学期三月月考文科数学试卷(解析版) 题型:填空题
设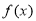 是定义在
是定义在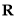 上的增函数,且对于任意的
上的增函数,且对于任意的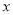 都有
都有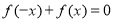 恒成立. 如果实数
恒成立. 如果实数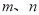 满足不等式
满足不等式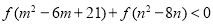 ,xxk那么
,xxk那么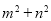 的取值范围是
的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com