
【题目】如图,矩形![]() (
(![]() ),被截去一角(即
),被截去一角(即![]() ),
),![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.
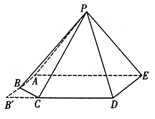
(1)求五棱锥![]() 的体积的最大值;
的体积的最大值;
(2)在(1)的情况下,证明: ![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)过![]() 作
作![]() ,由面面垂直性质定理得
,由面面垂直性质定理得![]() 平面
平面![]() ,即为五棱锥
,即为五棱锥![]() 的高,再利用平几知识计算底面面积,由
的高,再利用平几知识计算底面面积,由![]() 得
得![]() 在以
在以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆上,由椭圆的简单的几何性质知:点
的椭圆上,由椭圆的简单的几何性质知:点![]() 为短轴端点时,
为短轴端点时, ![]() 到
到![]() 的距离最大,最后代入锥体体积公式即可,(2)过
的距离最大,最后代入锥体体积公式即可,(2)过![]() 作
作![]() ,由面面垂直性质定理得
,由面面垂直性质定理得![]() 平面
平面![]() ,即得
,即得![]() ,再在平面
,再在平面![]() 内,根据平几知识计算可得
内,根据平几知识计算可得![]() .最后根据线面垂直判定定理得
.最后根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .
.
试题解析:(Ⅰ)解:因为![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
所以截去的![]() 是等腰直角三角形,
是等腰直角三角形,
所以![]() .
.
如图3,
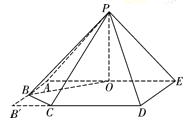
过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
, ![]() 为五棱锥
为五棱锥![]() 的高.
的高.
在平面![]() 内,
内, ![]() ,
, ![]() 在以
在以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆上,
的椭圆上,
由椭圆的简单的几何性质知:点![]() 为短轴端点时,
为短轴端点时, ![]() 到
到![]() 的距离最大,
的距离最大,
此时![]() ,
, ![]() ,(指出即可,未说明理由不扣分)
,(指出即可,未说明理由不扣分)
所以![]() ,
,
所以![]() .
.
(Ⅱ)证明:连接![]() ,如图,据(Ⅰ)知,
,如图,据(Ⅰ)知, ![]() ,故
,故![]() 是等腰直角三角形,所以
是等腰直角三角形,所以![]() ,
,
所以![]() ,即
,即![]() .
.
由于![]() 平面
平面![]() ,所以
,所以![]() ,
,
而![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() ,
, ![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为4的直角三角形.
是面积为4的直角三角形.
(1)求该椭圆的离心率和标准方程;
(2)过![]() 做直线
做直线![]() 交椭圆于
交椭圆于![]() 两点,使
两点,使![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学家刘徽在《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的立体为“牟合方盖”,如图(1)(2),刘徽未能求得牟合方盖的体积,直言“欲陋形措意,惧失正理”,不得不说“敢不阙疑,以俟能言者”.约200年后,祖冲之的儿子祖暅提出“幂势既同,则积不容异”,后世称为祖暅原理,即:两等高立体,若在每一等高处的截面积都相等,则两立体体积相等.如图(3)(4),祖暅利用八分之一正方体去掉八分之一牟合方盖后的几何体与长宽高皆为八分之一正方体的边长的倒四棱锥“等幂等积”,计算出牟合方盖的体积,据此可知,牟合方盖的体积与其外切正方体的体积之比为( )
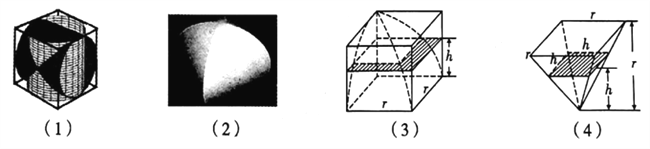
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘车补贴标准如下表:

某校研究性学习小组,从汽车市场上随机选取了![]() 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程![]() (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:

(1)求![]() 的值;
的值;
(2)若从这![]() 辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为![]() (单位:万元),求
(单位:万元),求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com